Другие алгоритмы
Существуют и другие алгоритмы.
Например, алгоритм Second-Chance - модификации FIFO, которая позволяет избежать потери часто используемых страниц - анализ бита r (reference) для самой старой страницы. Если бит 1, то страница в отличие от FIFO не выталкивается, а очищается бит и страница становится в конец очереди. Если на все страницы ссылались, он превращается в FIFO. Данный алгоритм использовался в BSD Unix.
В компьютере Макинтош использован алгоритм NRU (Not Recently-Used), где страница выбирается на основе анализа битов модификации и ссылки.
Что делать, если в распоряжении процесса имеется недостаточное число кадров? Следует ли его приостановить с освобождением всех его кадров. Что нужно понимать под достаточным количеством кадров?
Хотя теоретически возможно уменьшить число кадров процесса до минимума, существует какое-то число активно используемых страниц, без которого процесс часто генерирует falt’ы (рис.11.2). Эта высокая частота страничных нарушений называется трешинг (trashing, иногда употребляется русский термин пробуксовка). Процесс находится в состоянии трешинга, если он больше времени занимается подкачкой страниц, нежели выполнением. Критическая ситуация такого рода возникает вне зависимости от конкретных алгоритмов замещения.
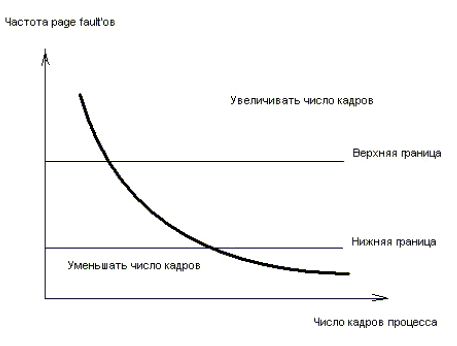
Рисунок 11.2 - Частота page fault'ов
Часто результатом трешинга является снижение производительности. Один из нежелательных сценариев развития событий может выглядеть следующим образом. При глобальном алгоритме замещения, процесс, которому не хватает кадров, начинает отбирать их у других процессов, а те в свою очередь начинают заниматься тем же. В результате все процессы попадают в очередь запросов к устройству вторичной памяти, а очередь процессов в состоянии готовности пустеет. Загрузка процессора снижается. Процессор видит это и увеличивает степень мультипрограммирования. Таким образом, пропускная способность системы падает из-за трешинга.
Эффект трешинга, возникающий при использовании глобальных алгоритмов, может быть ограничен за счет использования локальных алгоритмов замещения. Если даже один из процессов попал в трешинг, это не сказывается на других процессах. Однако он много времени проводит в очереди к устройству выгрузки, затрудняя подкачку страниц остальных процессов.
Критическая ситуация типа трешинга возникает вне зависимости от конкретных алгоритмов замещения. Единственным алгоритмом, теоретически гарантирующим отсутствие thrashing, является рассмотренный выше не реализуемый на практике оптимальный алгоритм.
Итак, трешинг - высокая частота страничных нарушений. Необходимо ее контролировать. Когда она высока, процесс нуждается в кадрах. Можно, устанавливая желаемую частоту fault'ов, регулировать размер процесса, добавляя или отнимая у него кадры. Как и в случае с рабочим множеством может оказаться целесообразным придержать процесс, освободив его кадры. Освободившиеся кадры выделяются другим процессам с высокой частотой fault'ов.
Для предотвращения трешинга нужно выделить процессу столько кадров, сколько ему нужно. Но как узнать, сколько ему нужно. Существует несколько подходов. Необходимо попытаться выяснить, как много кадров процесс реально использует. Этот подход определяет модель локальности выполнения процесса.
Концепция локальности
Суть концепции локальности изложена во введении. Изучая свойства локальности в пейджинговых системах, Деннинг сформулировал теорию рабочего множества программ.
Модель локальности состоит в том, что когда процесс выполняется, он двигается от одной локальности к другой. Локальность - набор страниц, которые активно используются вместе. Программа обычно состоит из нескольких различных локальностей, которые могут перекрываться. Например, когда вызвана процедура, она определяет новую локальность, состоящую из инструкций процедуры, ее локальных переменных, и множества глобальных переменных. После ее завершения процесс оставляет эту локальность, но может вернуться к ней вновь. Таким образом, локальность определяется кодом и данными программы. Заметим, что модель локальности - принцип, положенный в основу работы кэша. Если бы доступ к любым типам данных был случайным, кэш был бы бесполезным.
Если процессу выделять меньше кадров, чем ему нужно для поддержки его локальности он будет находиться в состоянии трешинга.
Модель рабочего множества (Working Set)
В варианте чистого пейджинга процессы стартуют без необходимых страниц в памяти. Первая же машинная инструкции генерирует page fault. Другой page fault происходит при локализации глобальных переменных и тут же при выделении памяти для стека. После того как процесс собрал большинство страниц, page fault'ы далее редки. Эта все происходит в соответствии с выборкой по запросу (требованию) в отличие от выборки с упреждением. Конечно, легко написать тестовую программу, которая систематически работает с большим адресным пространством. К счастью, большинство процессов не ведут себя подобным образом, а проявляют свойство локальности. В течение любой фазы вычислений процесс работает с небольшим количеством страниц. Этот набор называется рабочим множеством.
В некотором смысле предложенный Деннингом подход является практически реализуемой аппроксимацией оптимального алгоритма. Принцип локальности ссылок (недоказуемый, но подтверждаемый на практике) состоит в том, что если в период времени (T-t, T) программа обращалась к страницам (P 1, P 2,..., Pn), то при надлежащем выборе t с большой вероятностью эта программа будет обращаться к тем же страницам в период времени (T, T +t). Другими словами, принцип локальности утверждает, что если не слишком далеко заглядывать в будущее, то можно хорошо его прогнозировать исходя из прошлого. Набор страниц (P 1, P 2,..., Pn) и есть рабочее множество программы (или, правильнее, соответствующего процесса) в момент времени T. С течением времени рабочий набор процесса может изменяться как по составу страниц, так и по их числу.
Наиболее важное свойство рабочего множества - его размер. ОС выделяет каждому процессу достаточное число кадров, чтобы поместилось рабочее множество. Если еще остались кадры, то может быть инициирован другой процесс. Если рабочие множества процессов не помещаются в память, и начинается трешинг, то один из процессов надо попридержать.
Решение о размещении процессов в памяти должно базироваться на размере его рабочего множества. Для впервые инициируемых процессов это решение может быть принято эвристически. Во время работы размер рабочего множества процесса динамически меняется. Система должна уметь определять: расширяет процесс свое рабочее множество или перемещается на новое рабочее множество. Если память мала, чтобы содержать рабочее множество процесса, то page fault'ов много.
В системах с разделением времени процессы часто перемещаются на диск. Что делать, когда процесс возвращается в память. Опять ждать пока он соберет свое рабочее множество? Поэтому многие системы хранят информацию о рабочих множествах процессов и загружают их, даже если процесс еще не стартовал (стратегия выборки с упреждением).
Размер рабочего множества может быть фиксированным, а может динамически настраиваться. Рассмотрим один из алгоритмов динамической настройки рабочего множества. При создании каждому процессу назначается минимальный размер рабочего множества, определяющий число страниц процесса, гарантированно находящихся в физической памяти при его выполнении. Если процессу требуется физических страниц больше, чем минимальный размер рабочего множества, и в наличии имеется свободная физическая память, то система будет увеличивать размер рабочего множества, но, не превышая максимального размера. Если же процессу требуется еще больше страниц, то дополнительные страницы будут выделяться за счет свопинга, без увеличения рабочего множества. Поскольку замещаемые страницы рабочего множества в действительности еще некоторое время могут оставаться в физической памяти, то они при необходимости могут быть возвращены в рабочее множество достаточно быстро, не требуя дисковых операций.
Когда свободной физической памяти становится слишком мало, система будет стремиться увеличить ее количество, урезая рабочие множества, размеры которых превышают минимальные.
В установившемся состоянии система следит за количеством исключительных ситуаций не присутствия страницы, вызываемых процессом. Если процесс генерирует page fault, и память не слишком заполнена, то система увеличит размер его рабочего множества. Если же процесс не вызывает исключительных ситуаций в течение некоторого времени, то система будет урезать его рабочее множество. При использовании таких алгоритмов система будет пытаться обеспечить наилучшую производительность для каждого процесса, не требуя никакой дополнительной настройки системы пользователем.
Идея алгоритма подкачки Деннинга (иногда называемого алгоритмом рабочих наборов) состоит в том, что операционная система в каждый момент времени должна обеспечивать наличие в основной памяти текущих рабочих наборов всех процессов, которым разрешена конкуренция за доступ к процессору. Полная реализация алгоритма Деннинга практически гарантирует отсутствие thrashing. Алгоритм реализуем (известна, по меньшей мере, одна его полная реализация, которая, однако, потребовала специальной аппаратной поддержки). На практике применяются облегченные варианты алгоритмов подкачки, основанных на идее рабочего набора.
 2014-02-02
2014-02-02 2671
2671








