Неравноточных измерений

Математическая обработка результатов прямых

Веса измерений. Неравноточными называют измерения, выполненные приборами различной точности, разным числом приемов, в различных условиях.

При неравноточных измерениях точность каждого результата измерений характеризуется своей среднеквадратической погрешностью. Наряду со средней квадратической погрешностью при обработке неравноточных измерений пользуются относительной характеристикой точности – весом измерения. Вес i -го измерения вычисляют по формуле

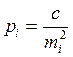(5.9)

где с – произвольная постоянная, назначаемая вычислителем, m_i – средняя квадратическая погрешность i -го измерения.

Так, имея ряд результатов измерений l ₁, l ₂,..., l_n, со средними квадратическими погрешностями m ₁ , m ₂,..., m_n, определяют их веса:

p ₁ = c / m ₁², p ₂ = c / m ₂² ,..., p_n = c / m_n ².

Часто постоянную с для удобства дальнейших вычислений назначают так, чтобы веса p_i оказались целыми числами.

Рассмотрим смысл произвольной постоянной с. Предположим, что в результате фиксирования значения с вес j -го измерения стал равен 1, то есть p_j = c / m_j ² = 1. Отсюда находим c = m_j ². Следовательно, постоянная с есть квадрат средней квадратической погрешности m² такого измерения, вес которого принят за единицу (с = m²).

Теперь (5.9) можем записать так

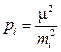. (5.10)

Кратко m называют средней квадратической погрешностью единицы веса.

Вес арифметической средины. Рассмотрим вес арифметической средины равноточных измерений. Примем в формуле (5.8) за единицу вес одного измерения, то есть m = m, и запишем .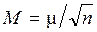

Тогда согласно (5.10) вес Р арифметической средины L будет равен

P = 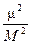= n. (5.11)

Вывод. Если за единицу веса принят вес одного измерения, то согласно (5.11) вес арифметической средины равен числу измерений.

Следствие. Если результат l измерения имеет вес р, то можем считать, что l является средним арифметическим из р измерений с весом 1.

Общая арифметическая средина результатов неравноточных измерений. Пусть имеем результаты многократных неравноточных измерений одной величины: l ₁, l ₂, …, l_n, выполненных с весами p ₁, p ₂, …, p_n.

Представим каждый из результатов l_i (i = 1, 2, …, n) как среднее из p_i результатов с весом 1. Получим такой ряд результатов равноточных измерений:

l ₁ - результат p ₁ измерений с весом 1,

l ₂ - результат p ₂ измерений с весом 1,

¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼

l_n - результат p_n измерений с весом 1,

где общее число измерений с весом 1 равно p ₁ + p ₂ +¼+ p_n.

Нами составлен ряд результатов равноточных измерений, позволяющий найти окончательное значение измеряемой величины как среднее арифметическое из всех результатов измерений

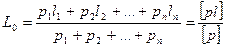. (5.12)

Значение, вычисляемое по формуле (5.12), называют общей арифметической срединой или весовым средним.

Оценки точности результатов неравноточных измерений. Приведем без вывода формулы характеристик точности, используемых при обработке прямых неравноточных измерений.

Средняя квадратическая погрешность m измерения, имеющего вес, равный единице:

- формула Гаусса: .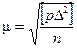

Формула применяется, когда известно достаточно точное, близкое к истинному, значение X измеряемой величины.

- формула Бесселя: ,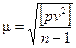

где v_i - поправки к результатам измерений:

.

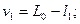
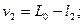
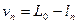Средняя квадратическая погрешность общей арифметической средины

Обработка результатов неравноточных измерений. Математическая обработка ряда результатов прямых неравноточных измерений одной величины выполняется в следующей последовательности.

1. Вычисление весового среднего (общей арифметической средины)

.

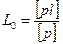2. Вычисление поправок к результатам измерений:

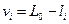(i = 1, 2,…, n).

Контролем правильности вычислений служит равенство

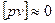
3. Вычисление средней квадратической погрешности одного измерения по уклонениям от арифметической средины, используя формулу Бесселя для неравноточных измерений:

.

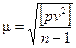4. Вычисление средней квадратической погрешности весового среднего

.