Перестановкой с повторениями называется размещение с повторениями по n из n элементов k -множества M (k £ n) со следующим дополнительным условием: различные k элементов множества M повторяются соответственно n 1,…, nk раз, 1£ n 1,…, nk £ n, n 1+…+ nk = n.
Теорема 6. Число перестановок с повторениями различных k элементов n 1,…, nk раз, 1£ n 1,…, nk £ n, n 1+…+ nk = n, равно 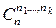 .
.
Доказательство. Пусть M – множество номеров перестановки с повторениями, одной из указанных в условии теоремы, M 1,…, Mk – множества номеров с одинаковыми элементами, повторяющимися n 1,…, nk раз соответственно. Тогда семейство множеств { M 1,…, Mk } будет разбиением множества M на k блоков. Значит, каждой перестановке с повторениями соответствует вполне определенное разбиение множества M на k блоков. Ясно, что это соответствие является биекцией. Значит, искомое число перестановок с повторениями равно числу разбиений на k блоков 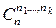 .
.
Задача 3. Найти число всех перестановок букв слова «баобаб».
Решение. n 1=3 (буква «б»), n 2=2 («а»), n 1=1 («о»), значит, 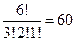 .
.
 2014-02-02
2014-02-02 2749
2749








