Тема: биномиальные коэффициенты
Основные вопросы, рассматриваемые на лекции:
1. Формула бинома Ньютона.
Свойства биномиальных коэффициентов:
2. следствия формулы числа сочетаний без повторений;
3. следствия формулы бинома Ньютона.
4. Разбиения на блоки. Полиномиальная формула.
5. Перестановки с повторениями.
Краткое содержание лекционного материала
1. Формула бинома Ньютона. Бином Ньютона (1+ x) n, после раскрытия скобок и приведения подобных, преобразуется в многочлен канонического вида a 0 xn + a 1 xn -1+…+ an -1 x 1+ anx 0, где a 0=1, an =1, x 0=1. Оказывается, что 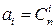 , где i =0,1,…, n. Поэтому числа сочетаний
, где i =0,1,…, n. Поэтому числа сочетаний 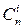 называются также биномиальными коэффициентами. Применятся обозначение:
называются также биномиальными коэффициентами. Применятся обозначение: 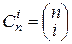 . Формула в следующей теореме называется формулой бинома Ньютона или биномом Ньютона.
. Формула в следующей теореме называется формулой бинома Ньютона или биномом Ньютона.
Теорема 1. 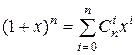 .
.
Доказательство. 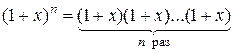 . Раскроем скобки и приведем подобные: в полученном многочлене коэффициент при степени xi равен сумме i единиц и n -i нулей. Число всевозможных выборов i единиц из общего числа выборов n равно
. Раскроем скобки и приведем подобные: в полученном многочлене коэффициент при степени xi равен сумме i единиц и n -i нулей. Число всевозможных выборов i единиц из общего числа выборов n равно 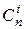 .
.
2. Свойства биномиальных коэффициентов как следствия формулы числа сочетаний без повторений. Используя формулу теоремы 5 лекции №5, можно доказать свойства биномиальных коэффициентов, которые мы приведем в следующей теореме.
Теорема 2.  ,
, 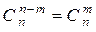 ,
, 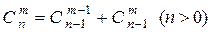 .
.
Доказательство. 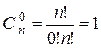 .
. 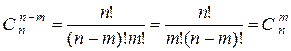 .
.
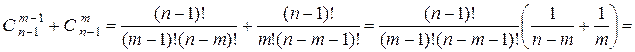
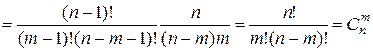 .
.
Задача 1. Найти все биномиальные коэффициенты для 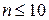 .
.
Решение запишем в виде треугольника Паскаля – бесконечной таблицы, имеющей треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы, так как  . Каждое внутреннее число равно сумме двух расположенных над ним чисел:
. Каждое внутреннее число равно сумме двух расположенных над ним чисел: 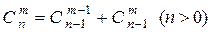 . Строки треугольника симметричны относительно вертикальной оси:
. Строки треугольника симметричны относительно вертикальной оси: 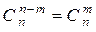 .
.
Биномиальный коэффициент 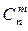 лежит на пересечении строки n и столбца m.
лежит на пересечении строки n и столбца m.
| m n | |||||||||||
3. Свойства биномиальных коэффициентов как следствия формулы бинома Ньютона. Используя формулу теоремы 1, можно доказать свойства биномиальных коэффициентов, которые мы приведем в следующей теореме.
Теорема 3. Имеют место следующие тождества:
1) 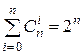 ;
;
2) 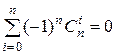 ;
;
3) 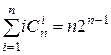 ;
;
4) 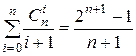 .
.
Доказательство. 1) В тождестве теоремы 1 подставим x =1.
2) В том же тождестве подставим x =-1.
3) Продифференцируем обе части того же тождества по x:
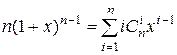 .
.
Затем подставим x =1.
4) Проинтегрируем обе части того же тождества по x от 0 до 1:
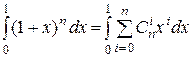 .
.
Получим: 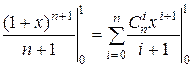 .
.
4. Разбиения на блоки. Полиномиальная формула. Разбиение n - множества на попарно непересекающиеся классы с известным набором 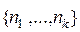 чисел элементов классов называется разбиением на блоки длины
чисел элементов классов называется разбиением на блоки длины 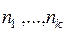 , где 1£ n 1, …, nk £ n, а n 1+…+ nk = n.
, где 1£ n 1, …, nk £ n, а n 1+…+ nk = n.
Теорема 4. Пусть 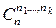 – число разбиений n -множества длины
– число разбиений n -множества длины 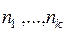 . Тогда
. Тогда 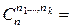
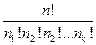 .
.
Доказательство. Пусть множество 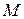 разбито на блоки M 1,…, Mk, такие, что | M 1|= n 1,…,| Mk |= nk, 1£ n 1,…, nk £ n, n 1+…+ nk = n.
разбито на блоки M 1,…, Mk, такие, что | M 1|= n 1,…,| Mk |= nk, 1£ n 1,…, nk £ n, n 1+…+ nk = n.
Элемент множества M 1 можно выбрать 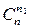 способами, элемент множества M 2 –
способами, элемент множества M 2 – 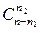 способами, элемент множества M 3 –
способами, элемент множества M 3 – 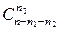 способами и т.д. Применим правило произведения:
способами и т.д. Применим правило произведения:
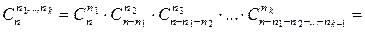
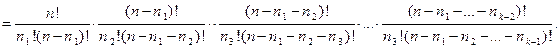
После сокращений получим: 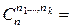
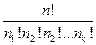 .
.
Докажем теорему о полиномиальной формуле.
Теорема 5. 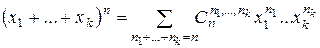 .
.
Доказательство. После раскрытия степени, подсчитываем число одночленов вида 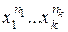 . Их столько же, сколько будет разбиений множества множителей
. Их столько же, сколько будет разбиений множества множителей 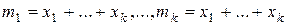 степени
степени 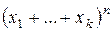 на подмножества, содержащие соответственно
на подмножества, содержащие соответственно 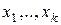 и имеющие мощность
и имеющие мощность 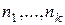 . Потому коэффициент при одночлене
. Потому коэффициент при одночлене 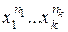 равен
равен 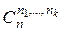 .
.
Формула, доказываемая в теореме 4, называется полиномиальной (или формулой полинома Ньютона).
Задача 2. Найти коэффициент 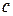 одночлена cx 2 y 3 z в многочлене, получаемом из степени
одночлена cx 2 y 3 z в многочлене, получаемом из степени 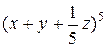 после раскрытия скобок и приведения подобных.
после раскрытия скобок и приведения подобных.
Решение. В силу теоремы 9,
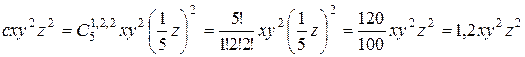 .
.
Ответ: 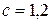 .
.
 2014-02-02
2014-02-02 4828
4828








