Тема: рекуррентные соотношения
Основные вопросы, рассматриваемые на лекции:
1. Определение рекуррентного соотношения. Примеры.
2. Общие и частные решения рекуррентных соотношений.
3. Линейные рекуррентные соотношения.
Краткое содержание лекционного материала
1. Определение рекуррентного соотношения. Примеры. Рекуррентным соотношением (или рекуррентной формулой) называется соотношение вида
 , (1)
, (1)
где  – функция, с помощью которой можно вычислить все члены последовательности
– функция, с помощью которой можно вычислить все члены последовательности 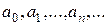 с заданными первыми
с заданными первыми 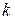 элементами
элементами 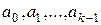 .
.
Последовательность 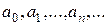 , получаемая с помощью соотношения (1), называется рекуррентной (recurrere (лат.) – возвращаться).
, получаемая с помощью соотношения (1), называется рекуррентной (recurrere (лат.) – возвращаться).
Примеры. 1) Соотношение 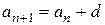 определяет арифметическую прогрессию с разностью
определяет арифметическую прогрессию с разностью  и с начальным членом a
и с начальным членом a 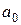 .
.
2) Соотношение an +1= an × q определяет геометрическую прогрессию со знаменателем q ¹0 и с начальным членом a 0.
3) Соотношение an +2= an + an +1 с начальными элементами a 0= a 1=1 задает последовательность Фибоначчи.
В 1202 году Леонардо из Пизы, известный как Фибоначчи – сын Боначчи, написал сочинение «Liber abacci», в котором была задача: «Предположим, что через месяц от одной пары кроликов порождает еще одна пара кроликов, а рождают кролики со второго месяца рождения. Имеется одна пара кроликов. Сколько пар кроликов будет через один год?»
Число новорожденных пар равно числу кроликов два месяца назад (an). Чтобы получить число кроликов в этом месяце (an +2), надо к этому числу прибавить число кроликов месяц назад (an +1). Следовательно, последовательность чисел пар кроликов по месяцам определяется соотношением an +2= an + an +1 с начальными элементами a 0=1 и a 1=1.
Месяц  | ||||||||||||
Число пар кроликов через месяц  |
 2014-02-02
2014-02-02 2009
2009
