2014-02-02
504
Закон больших чисел.
В широком смысле слова закон больших чисел означает, что при большом числе случайных экспериментов средний их результат практически перестает быть случайным и может быть предсказан с большой степенью определенности (т.е. событие имеет вероятность, близкую к 0 или 1).
В узком смысле под законом больших чисел в теории вероятности понимают ряд теорем, в которых устанавливается факт приближения различных характеристик большого числа опытов к некоторым постоянным (т.е. доказывается, что вероятность отклонения от них стремится к 1).
Пусть X – cлучайная величина с заданным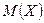и 
и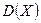 
. Тогда для 
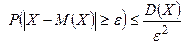. (1)
Неравенство оценивает вероятность того, что отклонение случайной величины X от центра распределения - 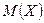превзойдет заданное определенное значение. Эта вероятность тем меньше, чем меньше .
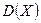Замечание. Оценка получается достаточно грубой, но зато это значение пригодно для любых случайных величин.
Пример 1. Пусть X – случайная величина, m = ,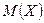
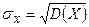. Используя неравенство Чебышева оценить 
.
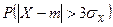Решение: Пусть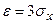 
, тогда 
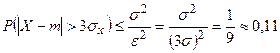. Но если случайная величина распределена по нормальному закону, то P= 0,003 (правило «трех сигм»).
Определение: Говорят, что случайная величина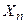 
сходится по вероятности к а, если при всех достаточно больших n выполняется неравенство:
или: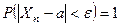 
,
где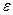 
- произвольное малое положительное число, а 
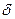зависит от выбора 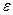и n.
