Пусть  независимые случайные величины, для которых существуют конечные
независимые случайные величины, для которых существуют конечные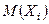 и
и 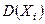 ,
, 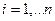 и центральный момент третьего порядка -
и центральный момент третьего порядка -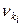 , причем
, причем
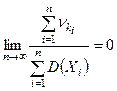 , (4)
, (4)
тогда их сумма с достаточной степенью точности имеет нормальное распределение.
Смысл условия (4) состоит в том, что действие каждого слагаемого (случайной величины) невелико по сравнению с суммарным действием их всех. Многие случайные явления, встречающиеся в природе и в общественной жизни, протекают именно по такой схеме. В связи с этим теорема Ляпунова имеет исключительно большое значение, а нормальный закон распределения является одним из основных законов в теории вероятностей.
Примеры.
4. При стрельбе из орудия под влиянием очень большого числа причин случайного характера происходит рассеяние снарядов на некоторой площади. Случайные воздействия на траекторию снаряда можно считать независимыми. Каждая причина вызывает лишь незначительное изменение траектории по сравнению с суммарным изменением под воздействием всех причин. Поэтому следует ожидать, что отклонение места разрыва снаряда от цели будет случайной величиной, распределенной по нормальному закону.
5. По теореме Ляпунова можно предположить, что, например, рост взрослого мужчины является случайной величиной, распределенной по нормальному закону. Эта гипотеза хорошо согласуется с наблюдениями. В подтверждение приведено распределение по росту 1000 взрослых рабочих мужчин и соответствующие теоретические численности мужчин, т. е. число мужчин, которые должны иметь рост указанных групп, если исходить из предположения о распределении роста мужчин по нормальному закону.
| Рост, см | экспериментальные данные | теоретические прогнозы |
| 143—146 | ||
| 146—149 | ||
| 149—152 | ||
| 152—155 | ||
| 155—158 | ||
| 158— 161 | ||
| 161— 164 | ||
| 164—167 | ||
| 167—170 | ||
| 170—173 | ||
| 173—176 | ||
| 176—179 | ||
| 179 —182 | ||
| 182—185 | ||
| 185—188 |
Более точного совпадения экспериментальных данных с теоретическими трудно было ожидать.
 2014-02-02
2014-02-02 689
689







