Теорема 2. Теорема Чебышева

Пусть X – cлучайная величина с заданным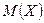и и 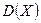. Тогда, при неограниченном увеличении количества независимых опытов, среднее арифметическое наблюдаемых значений случайной величины сходится по вероятности к ее математическому ожиданию, т.е.

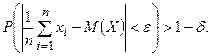(2)

В этом неравенстве можно принять 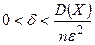, где 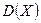- дисперсия случайной величины X.

Пример 2. Пусть в результате 100 независимых опытов найдены значения случайной величины X: 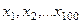. Пусть 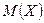=10, 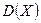=1. Оценить снизу вероятность того, что абсолютная величина разности между средним арифметическим наблюдаемых значений случайной величины 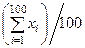и математическим ожиданием будет меньше .

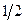Решение:

Воспользуемся неравенством (2):

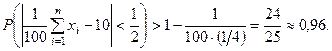
Таким образом, искомая вероятность больше 0,96.

Теорема Чебышева является одним из законов больших чисел, которые лежат в основе многих практических применений теории вероятностей.

Другим и притом простейшим (и ранее всех установленным) законом больших чисел является теорема Я. Бернулли.