В общем случае напряженного состояния

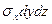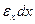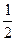
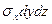
Потенциальная энергия, накопленная в элементарном объёме, определяется суммой работ сил, распределённых по поверхности этого объёма (рис.4.16). Нормальная силана грани перпендикулярной оси х совершит работу на перемещении , равную 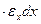, где 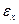- относительная линейная деформация вдоль оси х, вызванная всеми действующими силами.

Аналогичные работы совершат и остальные нормальные силы, действующие по граням перпендикулярным осям у и х: , .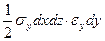

Касательная сила dxdz на площадке перпендикулярной оси y совершит работу на перемещении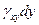, равную . Аналогичные выражения работ дают и касатель-

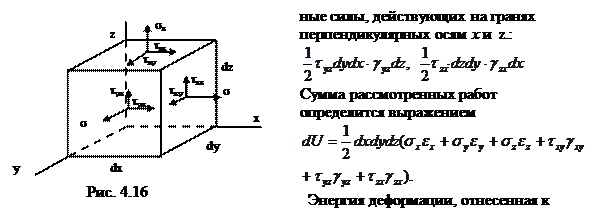
альной энергией и будет равна

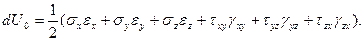
Используя выражения закона Гука для деформаций (4.15), (4.16), окончательно полу-чим (4.18)

Для главных напряжений . (4.19)

4.9 Энергия изменения формы и объёма

Энергия деформации расходуется на изменение формы тела и его объёма U₀ =

Выведем выражения для этих энергий, которые потребуются в дальнейшем при изучении вопросов, связанных с пластическими деформациями и предельными напряженными состоя-ниями

Если тело подвергнуть всестороннему сжатию со средним напряжением 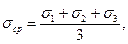то его форма изменяться не будет, а будет меняться только объём. В этом случае

После преобразования получим 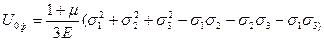(4.20)