Обратная задача.
Прямая задача
Аналитическое решение прямой задачи определяется формулами (4.6) – (4.9).
Для графического решения строится на плоскости в координатах s-t круг Мора
(рис. 4.9) в следующей последовательности.
|
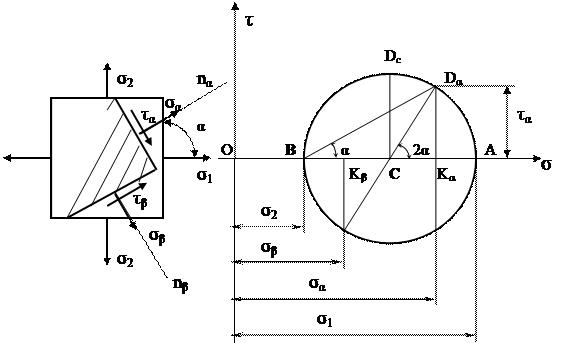 |
Выбирается прямоугольная система координат так, чтобы ось абсцисс была параллельна большему из главных напряжений s1, по этой оси в выбранном масштабе откладывются отрезки ОА и ОВ, численно равные напряжениям s1 и s2, а на их разности (на отрезке АВ) как на диаметре проводим окружность с центром в точке С.
Из крайней левой точки (В) круга проводим луч, параллельный внешней нормали к рассматриваемой площадке, т.е. под углом a к оси s. Точка пересечения этого луча с окружностью (Da) имеет своими координатами отрезки DaKa и OKa, численно равные касательному ta и нормальному sa напряжениям, действующим на рассматриваемой площадке.
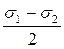 ,
, 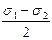 cos2α
cos2α 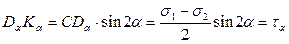
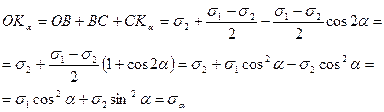
Точка Db, лежащая на противоположном конце диаметра от точки Da, характеризует напряжения sβ и tb, действующие по наклонной площадке, перпендикулярной к первой.
|
|
|
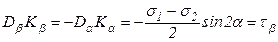
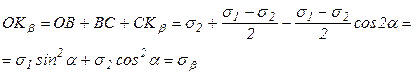
Выполненные преобразования проведены с учетом, что 1+cos2α = 2cos2α., 1-cos2α = 2sin2α.
Полученные выражения для sa, sb, τα и τβ полностью совпадают с аналитическими формулами (4.6) - (4.9).
В заключение следует отметить, что каждая точка круга Мора имеет своими координатами напряжения, действующие на соответствующей площадке, следовательно, зная главные напряжения для плоского напряженного состояния, можно с помощью круга Мора определить напряжения, действующие на различных площадках, проходящих через данную точку. Максимальное касательное напряжение соответствует точке Dc и равно радиусу круга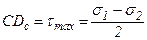 .
.
Довольно часто приходится решать обратную задачу, т. е. по напряжениям на произвольных площадках sa, ta, sb, tb определять величину и направление главных напряжений. Проще эта задача решается графически, т. е. с помощью круга Мора (рис. 4.10). Рассмотрим порядок его построения.
Прямоугольную систему координат s, t выберем так, чтобы ось абсцисс была параллельна большему из нормальных напряжений (пусть sa > sb). На оси s отложим в выбранном масштабе отрезки ОКa, ОКb, численно равные sa и sb. Из точек Кa и Кb проведем перпендикуляры КaDa, КbDb, которые численно равны соответственноta и τβ (КaDa = ta, КbDb = τβ = - ta). На отрезке DaDb, как на диаметре, построим круг с центром в точке С. Крайнюю правую точку пересечения круга с осью s обозначим буквой А, крайнюю левую – буквой В. Касательные напряжения в этих точках равны нулю, следовательно, ОА=s1, ОВ=s2 – главные напряжения (.в соответствии с прямой задачей).
|
|
|

Рис. 4.10
параллельна большему из нормальных напряжений (пусть sa > sb). На оси s отложим в выбранном масштабе отрезки ОКa, ОКb, численно равные sa и sb. Из точек Кa и Кb проведем перпендикуляры КaDa, КbDb, которые численно равны соответственноta и τβ (КaDa = ta, КbDb = τβ = - ta). На отрезке DaDb, как на диаметре, построим круг с центром в точке С. Крайнюю правую точку пересечения круга с осью s обозначим буквой А, крайнюю левую – буквой В. Касательные напряжения в этих точках равны нулю, следовательно, ОА=s1, ОВ=s2 – главные напряжения (.в соответствии с прямой задачей).
Из рис.6.10 определим радиус круга R и величину отрезка ОС 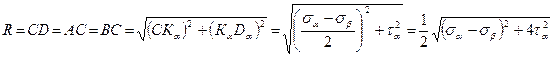 (4.12)
(4.12)
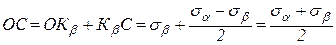 (4.13)
(4.13)
C учетом выражений (4.12), (4.13) получим следующие формулы для главных напряжений
ОА= σI = ОС + R = 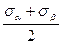 +
+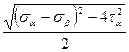 (4.14)
(4.14)
ОВ = σII = ОС – R = 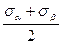 -
- 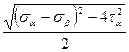 (4.15)
(4.15)
Или 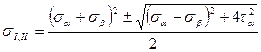 (4.16)
(4.16)
Для определения направления главного напряжения s1 проведем луч через крайнюю левую точку круга В и точку Da¢, которая симметрична точке Da относительно оси s. Направление луча ВDa¢ совпадает с направлением s1, направление s2 перпендикулярно ему. Угол a0 определится из треугольника ВКaDa¢ (рис. 6.10):
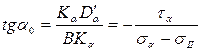 (4.17)
(4.17)
Угол a0 считается положительным, если его откладывают от оси s против часовой стрелки.
4.7 Напряжения на произвольной площадке при объемном напряженном состоянии
 В элементарном параллелепипеде, по граням которого действуют все три главных напряжения, рассмотрим произвольную площадку a, нормаль к которой составляет с координатными осями 1,2,3 углы α1 α2 α3.(рис. 4. 11). На этой площадке будет действовать полное напряжение рα, составляющее с нормалью n угол α. Определим его проекции на нормаль к площадке - σα и на саму площадку – τα.
В элементарном параллелепипеде, по граням которого действуют все три главных напряжения, рассмотрим произвольную площадку a, нормаль к которой составляет с координатными осями 1,2,3 углы α1 α2 α3.(рис. 4. 11). На этой площадке будет действовать полное напряжение рα, составляющее с нормалью n угол α. Определим его проекции на нормаль к площадке - σα и на саму площадку – τα.
|
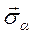 =
=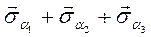 ,
, где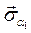 - напряжение на рассматриваемой площадке, вызванное действием
- напряжение на рассматриваемой площадке, вызванное действием  , а
, а  ,
,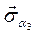 - соответственно от напряжений
- соответственно от напряжений 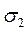 и
и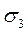 .Для вычисления этих величин воспользуемся формулой для линейного напряжённого состояния:
.Для вычисления этих величин воспользуемся формулой для линейного напряжённого состояния: 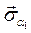 =
=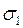
 ,
, 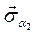 =
=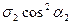 ,
, 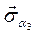 =
=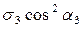 .
.
С учетом этих значений нормальные напряжения на произвольной площадке определятся равенством
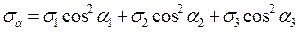 (4.18)
(4.18)
Для вывода формулы касательных напряжений τα следует рассмотреть его векторную величину 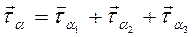 . Так как
. Так как 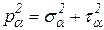 , то
, то  .
.
Опуская выводы, которые следуют из уравнений равновесия рассматриваемой трёх- гранной пирамиды (рис. 3.11), запишем формулу в окончательном виде для вектора полного напряжения на площадке nα:
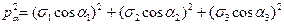 .
.
С учётом этого выражения
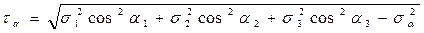 (4.19)
(4.19)
В качестве примера рассмотрим напряжения на площадке, равнонаклонённой ко всем главным площадкам. Такая площадка называется октаэдрической, а напряжения, действующие на этой площадке, называются октаэдрическими.
Так как для такой площадки 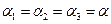 , а учитывая, что всегда
, а учитывая, что всегда
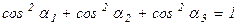 , то
, то 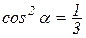 . Следовательно
. Следовательно 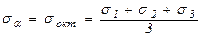 (4.20)
(4.20)
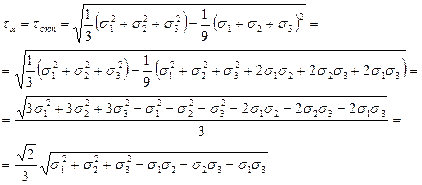 (4.21)
(4.21)
Так же, как и в случае плоского напряженного состояния, при объемном напряженном состоянии сумма нормальных напряжений по трем взаимно перпендикулярным площадкам, проходящим через рассматриваемую точку, есть величина постоянная.
Рассмотрим графический метод анализа напряженного состояния в точке при объемном напряженном состоянии.
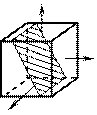
Прежде всего определим напряжения на площадках, параллельных одному из главных напряжений (рис. 4.12)
| |||||
| |||||
|
 |
 | |||
 |
а) б) в)
Рис.4.12
На площадках, параллельных s1, (рис. 4.12, а), напряжения зависят только от s2 и s3 и не зависят от s1, т. к. 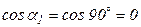 , тогда согласно (4.18)
, тогда согласно (4.18)
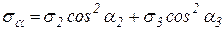
 |
Рис. 4.13.
Круг Мора, соответствующий этому случаю, представлен на рис. 4.13 кругом «а».
Напряжения в семействе площадок, параллельных s2, определяются по кругу «б», а в семействе площадок, параллельных s3 – с помощью круга «в».
В теории упругости доказывается, что площадкам общего положения соответствуют точки, лежащие в заштрихованной области (рис. 4.13).
|
|
|
Из представленного рисунка следует, что наименьшее и наибольшее нормальные напряжения равны наименьшему и наибольшему главным напряжениям 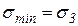 ,
, 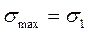 .
.
Наибольшие касательные напряжения равны радиусу наибольшего круга
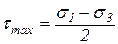
и действуют по площадке, равнонаклонённой к площадкам максимального и минимального из главных напряжений (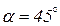 ).
).
 2014-02-02
2014-02-02 7404
7404
