Напряжения и перемещения в вале прямоугольного
Кручение брусьев некруглого поперечного сечения.
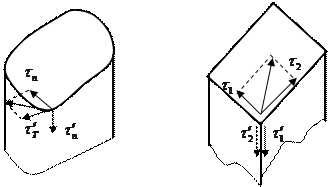
Задачи определения напряжений и деформаций при кручении брусьев некруглого поперечного сечения нельзя решить методами сопротивления материалов. Эти задачи рассматриваются в теории упругости. Причина этого в том, что у таких брусьев гипотеза плоских сечений не применима, так как поперечные сечения заметно искривляются, что и приводит к существенному изменению распределения напряжений.
Отметим некоторые закономерности распределения напряжений в сечениях некруглой формы, а затем приведем готовые решения, полученные методами теории упругости для некоторых форм поперечных сечений. Прежде всего, покажем, что касательные напряжения в поперечных сечениях для точек вблизи контура направлены по касательной к нему. Для этого
положим, что в некоторой точке А касательное напряжение τ направлено под углом, тогда его можно разложить по направлениям касательной
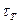
и нормали
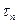
к контуру сечения (7.12, а). По закону парности касательных напряжений на поверхности стержня должно возникнуть напряжение
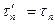
, но эта поверхность свободна от нагрузки, следовательно,
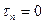
,
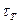
направлено по касательной к контуру.
Аналогично можно показать, что в сечении с внешними углами напряжения равны нулю. Разложим напряжения вблизи угла на две составляющие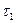 и
и 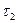 (7.12,б), так как парные им напряжения
(7.12,б), так как парные им напряжения 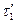 и
и 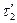 равны нулю, то и в ноль обращаются
равны нулю, то и в ноль обращаются 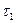 и
и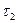 . Значит, вблизи внешнего угла касательные напряжения в поперечном сечении отсутствуют.
. Значит, вблизи внешнего угла касательные напряжения в поперечном сечении отсутствуют.
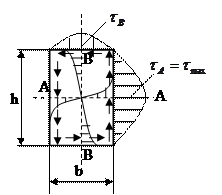 На рис. 7.13 показана эпюра касательных напряжений для бруса прямоугольного сечения, полученная методами теории упругости. Как видим, в углах напряжения равны нулю, а наибольшей величины они достигают в точках А по средине больших сторон:
На рис. 7.13 показана эпюра касательных напряжений для бруса прямоугольного сечения, полученная методами теории упругости. Как видим, в углах напряжения равны нулю, а наибольшей величины они достигают в точках А по средине больших сторон:
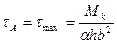 , (7.15)
, (7.15)
в точках В касательные напряжения вычисляются по формуле:

.
Здесь h – размер большой стороны, b – размер меньшей
стороны прямоугольника.
Коэффициенты α, β и η зависят от отношения сторон h/b.
Угол закручивания находится из выражения 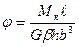 . (7.16)
. (7.16)
Коэффициент 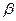 так же является функцией отношения сторон. При h/b≥10
так же является функцией отношения сторон. При h/b≥10 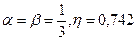 .
.
Таблица
| h/b
|
| 1,5
| 1,75
|
| 2,5
|
|
|
|
|
|  ∞ ∞
|
 α α
| 0,208
| 0,231
| 0,239
| 0,246
| 0,258
| 0,267
| 0,282
| 0,299
| 0,307
| 0,313
| 0,333
|
| β
| 0,141
| 0,196
| 0,214
| 0,229
| 0,249
| 0,263
| 0,281
| 0,299
| 0,307
| 0,313
| 0,333
|
| η
| 1, 00
| 0,859
| 0,82
| 0,795
| 0,766
| 0,753
| 0,745
| 0,743
| 0,742
| 0,742
|
|

Для формул (7.15), (7.16) введем геометрические параметры:
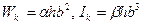 ,
,
тогда они примут вид
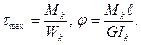
 Задачи определения напряжений и деформаций при кручении брусьев некруглого поперечного сечения нельзя решить методами сопротивления материалов. Эти задачи рассматриваются в теории упругости. Причина этого в том, что у таких брусьев гипотеза плоских сечений не применима, так как поперечные сечения заметно искривляются, что и приводит к существенному изменению распределения напряжений.
Задачи определения напряжений и деформаций при кручении брусьев некруглого поперечного сечения нельзя решить методами сопротивления материалов. Эти задачи рассматриваются в теории упругости. Причина этого в том, что у таких брусьев гипотеза плоских сечений не применима, так как поперечные сечения заметно искривляются, что и приводит к существенному изменению распределения напряжений.
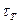 и нормали
и нормали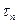 к контуру сечения (7.12, а). По закону парности касательных напряжений на поверхности стержня должно возникнуть напряжение
к контуру сечения (7.12, а). По закону парности касательных напряжений на поверхности стержня должно возникнуть напряжение 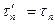 , но эта поверхность свободна от нагрузки, следовательно,
, но эта поверхность свободна от нагрузки, следовательно, 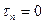 ,
, 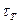 направлено по касательной к контуру.
направлено по касательной к контуру.
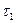 и
и 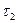 (7.12,б), так как парные им напряжения
(7.12,б), так как парные им напряжения 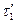 и
и 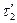 равны нулю, то и в ноль обращаются
равны нулю, то и в ноль обращаются 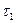 и
и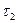 . Значит, вблизи внешнего угла касательные напряжения в поперечном сечении отсутствуют.
. Значит, вблизи внешнего угла касательные напряжения в поперечном сечении отсутствуют. На рис. 7.13 показана эпюра касательных напряжений для бруса прямоугольного сечения, полученная методами теории упругости. Как видим, в углах напряжения равны нулю, а наибольшей величины они достигают в точках А по средине больших сторон:
На рис. 7.13 показана эпюра касательных напряжений для бруса прямоугольного сечения, полученная методами теории упругости. Как видим, в углах напряжения равны нулю, а наибольшей величины они достигают в точках А по средине больших сторон: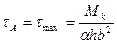 , (7.15)
, (7.15) .
.
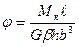 . (7.16)
. (7.16)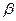 так же является функцией отношения сторон. При h/b≥10
так же является функцией отношения сторон. При h/b≥10 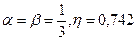 .
. ∞
∞
 α
α

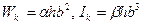 ,
,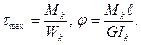
 2014-02-02
2014-02-02 685
685








