Главными требованиями к компаратору являются быстродействие и точность. Смещение компаратора не влияет на линейность АЦП, поскольку оно проявляется как смещение характеристики преобразования. Кроме того, обычным является применение способов уменьшения смещения нуля. Шум, однако, остается и компаратор обычно разрабатывается так, чтобы иметь шум не более 1 LSB. Дополнительно от компаратора требуется различать напряжения с точностью всей системы, т.е. компаратор должен быть настолько же точным, как весь АЦП.
3.4 Сигма-дельта АЦП [Д5]
Сигма-дельта АЦП обеспечивают высокое разрешение, высокую интеграцию при низкой стоимости, что делает их выбор оптимальным для таких применений, как управление процессами и взвешенные шкалы. Однако разработчики часто склоняются в пользу АЦП последовательного применения потому, что они не понимают работу сигма-дельта АЦП.
Аналоговая часть сигма-дельта АЦП очень проста – это 1- разрядный АЦП, однако цифровая часть, которая делает этот тип АЦП таким дешевым в производстве, весьма сложна. Она выполняет фильтрацию и децимацию. Чтобы понять, как это осуществляется, читателю необходимо ознакомиться с концепциями перевыборки (oversampling), формирования шумов, цифровой фильтрации и децимации.
Перевыборка (oversampling)
Сначала рассмотрим частную передаточную функцию традиционного многоразрядного АЦП при входном сигнале синусоидальной формы. Входной сигнал выбирается с частотой Fs. В соответствии с теорией Найквиста Fs должна быть по меньшей мере в два раза больше полосы входного сигнала.
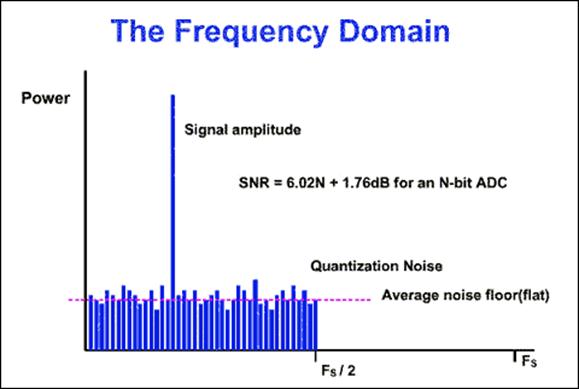
Рис.3.4.1
При рассмотрении результатов Фурье-анализа выходного цифрового сигнала мы увидим одиночную спектральную линию и массу шума, протянувшегося от нулевой частоты до Fs/2 (Рис.3.4.1). Известный под названием шума квантования этот эффект возникает в результате следующего: входной сигнал – непрерывный с бесконечным числом возможных состояний, а выходной – дискретная функция. Чье число возможных состояний определяется разрешением АЦП. Итак, при преобразовании сигнала из аналоговой формы в цифровую теряется часть информации и вносятся искажения в сигнал. Искажения носят случайный характер с величиной в пределах ±LSB.
Если мы поделим амплитуду основной гармоники сигнала на среднеквадратическое значение всех частных составляющих шума квантования, то мы получим отношение сигнал/шум (SNR). Для N-разрядного АЦП SNR=6,02 N+1,76 дб. Для улучшения в обычном АЦП SNR (и, соответственно, точность воспроизведения сигнала) вы должны увеличивать число разрядов.
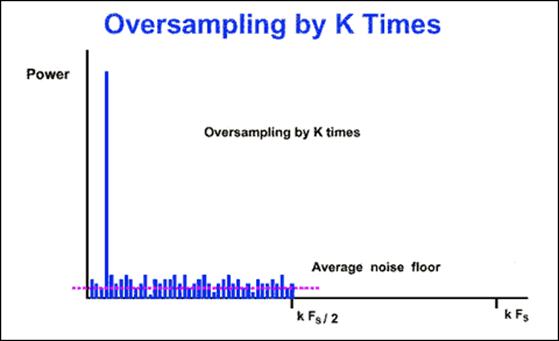
Рис.3.4.2
Рассмотрим снова предыдущий пример, но при увеличенной в k раз частоте выборки kFs (здесь k – коэффициент перевыборки). Фурье преобразование показывает снижение уровня шума (рис. 3.4.2). SNR здесь такой же, но энергия шума распределена в более широком диапазоне частот. Сигма дельта преобразователи используют этот эффект, совмещая 1-разрядный АЦП с цифровым фильтром (рис. 3.4.3), при этом малоразрядный АЦП обеспечивает широкий динамический диапазон.
Заметим, что SNR 1-разрядного АЦП равен 6,02+1,76 дб. Каждое увеличение частоты выборки в 4 раза увеличивает SNR на 6 дб, а каждые 6 дб увеличения SNR эквивалентны увеличению разрешения АЦП на 1 разряд. Одноразрядный АЦП с 24-кратной перевыборкой достигает разрешения 4-разрядного АЦП, для достижения 16 разрешения коэффициент перевыборки должен быть равен 415, что практически нереализуемо. Но сигма-дельта АЦП преодолевают это ограничение используя процедуру формирования шумов, которая позволяет получать большее, чем 6 дб, повышение SNR на каждое 4-кратное повышение частоты выборки.
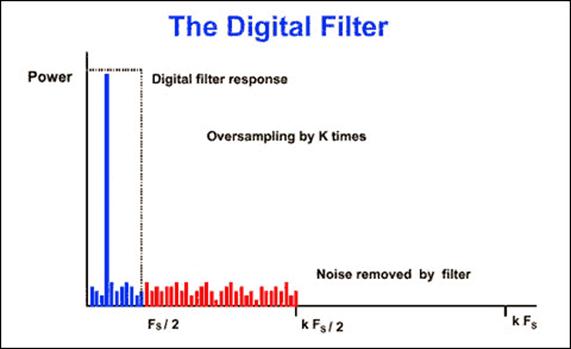
Рис.3.4.3
Формирование шумов
Чтобы понять процедуру формирования шумов, рассмотрим блок-схему сигма-дельта модулятора первого порядка (Рис.3.4.4). Он включает дифференциальный усилитель, интегратор и компаратор с обратной связью, которая осуществляется через 1-разрядный ЦАП. Этот ЦАП представляет собой просто ключ, который подключает инвертирующий вход дифференциального усилителя к положительному или отрицательному опорному напряжению. Задача ЦАП обратной связи – поддерживать выход интегратора в среднем около опорного уровня компаратора.
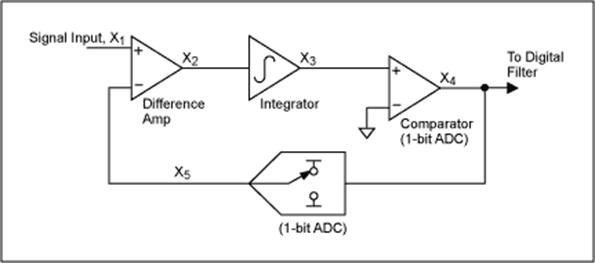
Рис.3.4.4
Плотность «1» в потоке выходных данных модулятора пропорциональна входному сигналу. При увеличении входного сигнала компаратор генерирует больше чисел «1» и наоборот - при уменьшении. Суммируя напряжение ошибки интегратор работает как фильтр нижних частот для входного сигнала и как фильтр верхних частот для шума квантования. Таким образом большая часть шума квантования выдается на верхних частотах (Рис.3.4.5). Перевыборка изменяет не общую энергию шумов, а ее распределение.
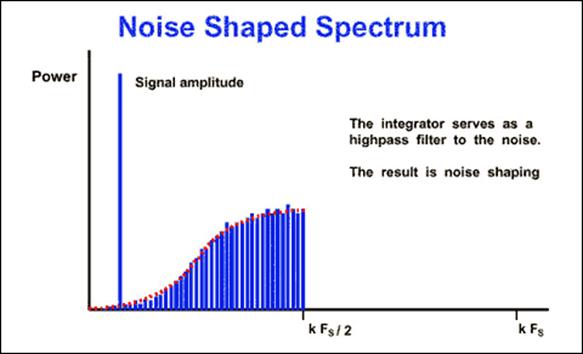
Рис.3.4.5
Если мы добавим цифровой фильтр к модулятору с формированием шумов, он удалит больше шумов, чем простая перевыборка (Рис.3.4.6). Этот тип модулятора (первого порядка) обеспечивает повышение SNR на 9 дб при каждом удвоении частоты выборки. Для более высокого порядка квантования мы можем включать более одной секции интегрирования и суммирования в сигма-дельта модулятор. Например, сигма-дельта модулятор второго порядка обеспечивает повышение SNR на 15 дб при каждом удвоении частоты выборки. На рис.3.4.7 показано соотношение между порядком сигма-дельта модулятора и коэффициентом перевыборки, необходимым для обеспечения заданного SNR.
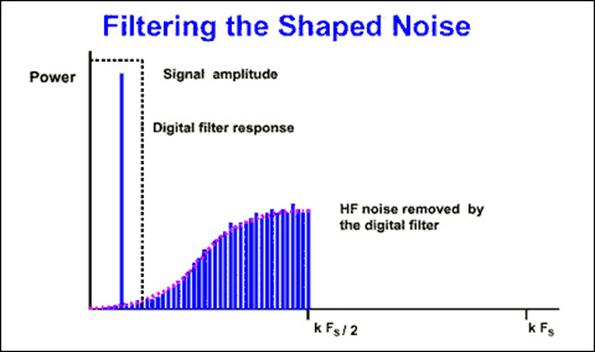
Рис.3.4.6
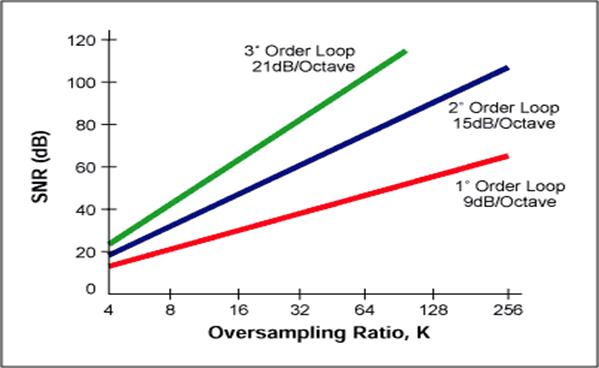
Рис.3.4.7
Цифровой и децимационный фильтры
Выходной сигнал модулятора представляет собой 1- разрядный поток данных с частотой выборки, которая может достигать мегагерц. Назначение цифрового и децимационного фильтров (Рис.3.4.8) – извлечь информацию из этого потока данных и снизить тем выдачи информации до более полезной величины. В сигма-дельта АЦП цифровые фильтры усредняют 1- разрядный поток данных, повышают разрешение АЦП и удаляют шум квантования, который выходит за пределы используемой полосы частот. Они определяют полосу сигнала, время установления и подавление вне полосы пропускания.
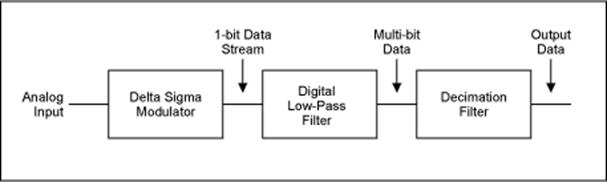
Рис.3.4.8
В сигма-дельта АЦП широко используется фильтр нижних частот с топологией Sinc3. Главное преимущество этого фильтра – его решетчатая частотная характеристика с глубокими провалами (Рис.3.4.9), фильтр (для примера) может подавить линию некоторой частоты, когда настроен на эту частоту. Положение провалов прямо связано с темпом выдачи выходных данных (1/период выдачи выходных слов). Фильтр устанавливается за три периода выдачи выходных слов. С частотой режекции 60 Гц (частота выдачи выходной информации 60 Гц) время установления равно 50 мс. Для применений, которые требуют низкое разрешение и быстрое установление выходной информации рассмотрим АЦП семейства МАХ1400, которые позволяют выбирать тип фильтра (Sinc1 или Sinc3).
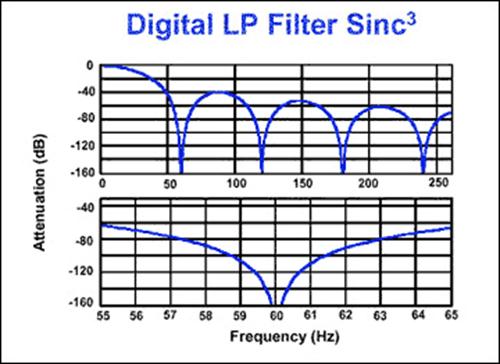
Рис.3.4.9
Время установления фильтра Sinc1 равно одному слову данных, т.е. для предыдущего примера 16,7 мс. Поскольку полоса передаваемых частот снижается выходным цифровым фильтром, темп выдачи выходных данных удовлетворяет критерию Найквиста не смотря на то, что он ниже исходной частоты выборки. Это может быть выполнено путем сохранения части входных выборок и отбрасывания остальных. Это процесс называют децимацией с коэффициентом М (отношение децимации). М может быть любой целой величиной, удовлетворяющей требованию, что частота выдачи выходных данных более чем в два раза больше полосы сигнала (Рис.3.4.10). Если частота входных выборок была Fs, то темп выдачи выходных данных может быть снижен до Fs/М без потери информации.
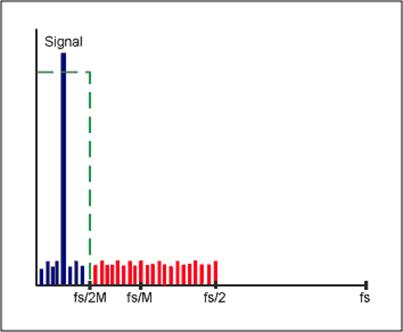
Рис.3.4.10
3.5 Интегрирующие АЦП [Д14]
Интегрирующие АЦП обеспечивают высокое разрешение и могут успешно подавлять шум и сосредоточенные помехи определенных частот. Интегрирующая архитектура обеспечивает прямой и понятный подход к преобразованию узкополосного аналогового сигнала в его цифровое представление. Этот тип АЦП находит широкое применение в портативной измерительной аппаратуре, включая цифровые панельные приборы и мультиметры.
Архитектура АЦП с одиночным интегрированием
Простейшие интегрирующие АЦП используют архитектуру с одиночным интегрированием (Рис.3.5.1). Здесь неизвестное входное напряжение интегрируется и интеграл сравнивается с известным опорным напряжением. Время до срабатывания компаратора пропорционально входному напряжению. В этой архитектуре высоки требования к точности и стабильности опорного напряжения для обеспечения точности измерения.

Рис.3.5.1
У этой архитектуры есть один существенный недостаток – ее точность зависит также от разброса величин резистора R и конденсатора С. Малейшие отклонения этих компонентов изменяют результат преобразования и затрудняют обеспечение повторяемости измерений. Для преодоления чувствительности к величинам компонентов используют архитектуру с двойным интегрированием.
Архитектура АЦП с двойным интегрированием
АЦП с двойным интегрированием интегрирует входное напряжение VIN в течение фиксированного времени TINT, затем “деинтегрирует”, используя известное опорное напряжение VREF за переменное время TDE-INT (Рис.3.5.2). Ключевое преимущество этой архитектуры перед предыдущей в том, что результат преобразования нечувствителен к величине компонентов. Т.е. ошибка, вносимая компонентами в течение цикла интегрирования, исключается в фазе деинтегрирования. Если выразить это в виде уравнения, то
VIN/ TINT= VREF/ TDE-INT или TDE-INT = TINT* (VIN/ VREF).
Для того, чтобы получить 10-разрядное разрешение мы должны интегрировать в течение 1024 тактовых циклов (210), затем деинтегрировать в течение 1024 циклов (210), обеспечивая преобразование максимального входного напряжения за 2*210 тактовых циклов. Для обеспечения большего разрешения надо увеличить число тактовых циклов. Взаимообмен между временем преобразования и разрешением является внутренним свойством этой архитектуры. Конечно, возможно ускорить преобразование при заданном разрешении за счет схемных ухищрений, однако при таких улучшениях точность начинает зависеть от согласования, внешних компонентов, инжекции заряда и т.п. Другими словами, все ускоренные структуры имеют гораздо больший бюджет погрешностей. Даже в простом АЦП рис.3.5.1 есть масса потенциальных источников погрешности: влияние питания, подавление помехи общего вида, конечное усиление усилителя, насыщение интегратора, быстродействие компаратора, генерация компаратора, утечки в конденсаторе, паразитные емкости и т.д.
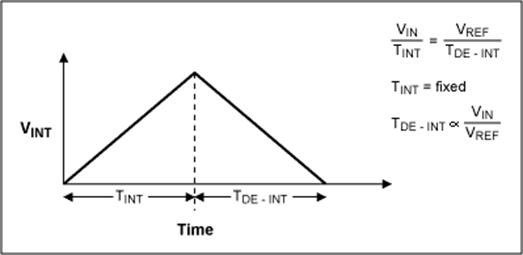
Рис.3.5.2
АЦП с многократным интегрированием
Разрешение АЦП с двойным интегрированием ограничивается быстродействием компаратора (при этом предполагается, что ошибка системы по постоянному току минимизирована проектированием усилителя с высоким коэффициентом усиления и обеспечением малой зависимости интегратора и компаратора от источников питания и помехи общего вида). Для 20-разрядного АЦП с тактовой частотой 1 МГц время преобразование составляет 2 секунды. При этом скорость изменения напряжения на входе компаратора составляет 2 микровольта за микросекунду. При такой малой скорости ошибка компаратора позволяет интегратору уйти от точки переключения на значительное расстояние. Этот выброс (измеренный на выходе интегратора) называется остатком. Очевидно, что такой АЦП не сможет обеспечить 20-разрядную точность.
Вместо этого мы можем преобразовать первые 10 значащих разрядов (один цикл интергирования-деинтегрирования), затем усилить остаток в 25 раз и деинтегрировать, затем снова усилить остаток в 25 раз и деинтегрировать его. Если остаток усилен правильно (т.е. малы инжекция заряда и другие ошибки), эта процедура может быть мощным инструментом для повышения разрешения и снижения времени преобразования. Результат преобразования в такой структуре формируется следующим образом: первое время деинтегрирования * 210 минус второе время деинтегрирования * 25 плюс третье время деинтегрирования * 20.
Глубокий анализ архитектуры
 2014-02-02
2014-02-02 1755
1755
