Геодезические задачи

Ориентирование линий. Прямая и обратная

Лекция 2.

Самостоятельное изучение.

Понятие о равноугольной проекции Гаусса-Крюгера и общегосударственной системе плоских прямоугольных координат

Литература: Лекции по инженерной геодезии (с фрагментами методического комплекса). Учебное пособие/ В.П. Абрамов; под редакцией О.С. Разумова. – Тула, 2005. С 8–9.

Ориентировать линию местности – значит определять ее направление относительно некоторого другого направления, принятого за исходное. В геодезии в качестве исходного принимаются направления: 1) истинного меридиана; 2) магнитного меридиана; 3) оси абсцисс или линии, ей параллельной. В этой связи различают три вида ориентирных углов для одной и той же линии.

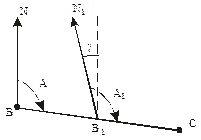Астрономический (истинный) азимут – горизонтальный угол А, отсчитанный в начальной точке линии по ходу часовой стрелки от северного направления истинного меридиана этой точки до заданного направления линии (рис.1.10). Угол А может принимать значения от 0° до 360°.

Азимут линии в разных ее точках меняется на угол g между направлением меридианов в этих точках. Этот угол называют сближением меридианов и, как следует из рис.1.10, А₁=А+g. Истинный азимут может быть определен на местности из астрономических наблюдений или при помощи гироскопического теодолита.

Для каждой линии принято различать прямые и обратные направления. Они отличаются друг от друга на 180° и угол g сближения меридианов, то есть

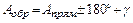. (12)

Сам угол равен 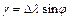, (13)

где Dl – разность долгот точек; j – средняя широта.

Магнитный азимут – горизонтальный угол A_m, отсчитанный в начальной точке линии от северного направления магнитного меридиана (магнитной стрелки) по направлению движения часовой стрелки до направления заданной линии. A_m может быть измерен на местности с помощью буссоли (компаса).

Дирекционный угол a отсчитывается от положительного направления оси абсцисс или линии, ей параллельной, по ходу часовой стрелки до заданного направления (рис.1.11). Прямой и обратный дирекционные углы отличаются друг от друга на 180°, то есть

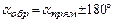. (14)

Ориентирные углы связаны друг с другом определенными соотношениями. Так, отклонение северного конца магнитной стрелки от направления истинного меридиана называется склонением d магнитной стрелки. Эта величина зависит от состояния магнитного поля Земли, которое непостоянно во времени. В районах магнитных аномалий значение d может изменяться в значительных пределах и ориентирование по магнитному азимуту там ненадежно.

Условно принято считать восточное склонение положительным, а западное отрицательным.

На рис.1.12 показано восточное склонение +d, и в общем случае связь между истинным и магнитным азимутом выражается формулой

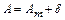, (15)

(в формулу (15) d входит со своим знаком).

Угол g, на который отклоняется в данной точке линия, параллельная оси абсцисс, от направления истинного меридиана, называется Гауссовым сближением меридианов. Как было сказано выше, в проекции Гаусса–Крюгера за ось абсцисс принимается осевой меридиан зоны, поэтому для точки с известными географическими координатами j и l Гауссово сближение меридианов может быть вычислено по формуле

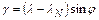, (16)

где l _N – долгота осевого меридиана зоны (10).

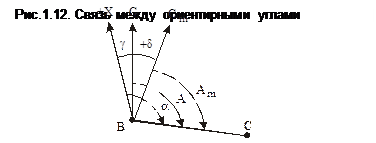Таким образом, для точек, лежащих к востоку от осевого меридиана, сближение меридиана положительное, а западное сближение отрицательное. На осевом меридиане и экваторе g=0°. Связь между истинным азимутом А и дирекционным углом a выражается соотношением

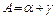(17)

(формула имеет алгебраический смысл).

На топографических картах под южной рамкой обычно указывается среднее значение склонения магнитной стрелки и Гауссова сближения меридианов.

Для ориентирования линий используют еще один ориентирный угол – румб (рис.1.13). Это острый горизонтальный угол r между ближайшим концом меридиана (или оси абсцисс) и направлением данной линии. Перед численным значением румба указывают его направление относительно сторон света. Связь между азимутами (дирекционными углами) и румбами показана в табл.1.1.

Таблица 1.1

Связь между румбами и дирекционными углами

Четверть	А (или a)	Румб r
	0° – 90°	СВ: r ₁=a₁
	90° – 180°	ЮВ: r ₂=180°-a₂
	180° – 270°	ЮЗ: r ₃=a₃-180°
	270° – 360°	СЗ: r ₄=360°-a₄

Прямая геодезическая задача состоит в вычислении координат точки 2 при известных координатах точки 1, расстоянию S ₁₂ и дирекционному углу линии 1-2 (рис.1.14).

Из треугольника 1С2 следует:

, ,

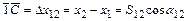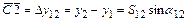где Dх₁₂и Dх₁₂– приращения координат.

Поэтому

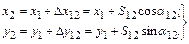(18)

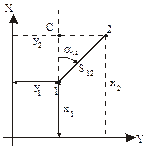Знаки у приращений координат определяются знаками тригонометрических функций cosa и sina.

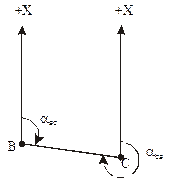
Обратная геодезическая задача заключается в определении длины линии S и ее дирекционного угла a по координатам концов этой линии, то есть в задаче дано x₁, y ₁, x ₂, y ₂. Требуется вычислить a₁₂и S ₁₂. Из треугольника 1 С 2 (см. рис.1.14) следует, что

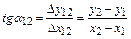, (19)

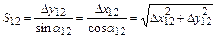. (20)

При решении этой задачи на калькуляторе по команде arctg на табло высвечивается значение румба данной линии в градусах и долях градуса. В соответствии со знаками приращений координат (знаки cos и sin) нужно по табл.1.2 определить номер четверти, в которой проходит линия, и от румба перейти к дирекционному углу (см. табл.1.1), выразив его в градусах, минутах и секундах дуги.

Таблица 1.2