Принцип независимости расширения каверны

НЕСТАЦИОНАРНЫЕ ОСЕСИММЕТРИЧНЫЕ КАВЕРНЫ.

Как уже отмечалось, течение в кормовой части каверны всегда нестационарно. В теоретических схемах это обстоятельство обычно игнорируется и вводится понятие стационарной каверны. В предыдущем параграфе в условиях 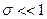, когда каверна представляет собой сильно вытянутую вдоль потока поверхность вра­щения, удалось установить простое дифференциальное уравнение (7.84), описывающее профиль каверны– R(x) в стационарном случае. Оно было получено в предположении, что течение в жид­ком слое, перпендикулярном набегающему потоку, практически не зависит от течения в смежных слоях, расположенных вверх или вниз по потоку. Конечность размеров конфигурации тело-ка­верна интегрально учитывается лишь коэффициентом 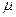. При этом оказалось, что радиус каверны в произвольном поперечном сече­нии x определяется четырьмя параметрами: сопротивлением тела--насадка 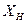, его размером 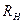, скоростью движения 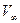и перепа­дом давления . Нетрудно представить, что отдельные из указанных параметров могут оказаться переменными либо в пространстве, либо во времени, либо одновременно в пространстве и времени. Например, давление окружающей среды 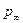в тяже­лой жидкости будет изменяться с глубиной, а на малой посто­янной глубине в условиях волнения будет зависеть от времени. Переменными во времени могут оказаться скорость движения кавернообразующего тела 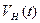, давление в каверне 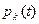. Вслед­ствие этого размер поперечного сечения каверны будет зависеть не только от продольной координаты, но и от времени. Так воз­никает проблема построения профиля нестационарной каверны.

Решение задачи эффективно достигается на основе принципа независимости расширения каверны, предложенного Логвиновичем. Суть его состоит в следу­ющем: закон расширения каверны в произвольном поперечном сечении не зависит от предыдущего и последующего движения кавернообразующего тела - насадка, а определяется размером 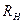, скоростью 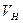и сопротивлением 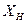насадка в момент прохожде­ния им плоскости наблюдения, а также перепадом давления 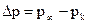. И поэтому к расчету нестационарной несимметричной каверны можно применить модифицированное дифференциальное уравнение стационарной каверны:

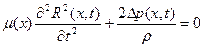(7.102)

с начальными условиями:

при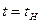

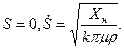(7.103)

Такой подход, естественно, должен иметь ограниченные пределы применимости. Экспериментальная проверка подтверждает его правомерность в широком диапазоне изменения параметров.

При анализе нестационарных каверн удобно использовать неподвижную систему координат 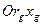и абсолютное время t. Вме­сте с тем целесообразно ввести подвижную; связанную с телом - насадком систему координат 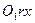и относительное время 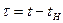. Пусть закон движения насадка описывается уравнением 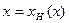. Обратная функция дает зависимость 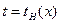. Связь между системами координат определяется очевидным соотношением

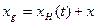(7.104)

Уравнение (7.102) при начальных условиях (7.103) допускает решение в виде:

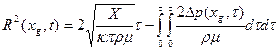. (7.105)