Кавитационные течения при угле атаки

Если вектор скорости набегающего потока образует некоторый угол δ (рис. 7.16) с продольной осью осесимметричного кавернообразующего элемен­та, то осевая симметрия течения нарушается. Вследствие этого на кавернообразующем элементе возникает поперечная сила, подъемная или топящая, в зависимости от знака угла атаки, ось каверны искривляется, поперечные сечения каверны деформируются.

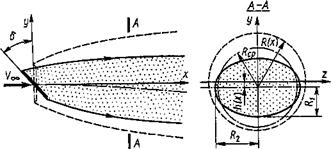
Рис. 7.16

Ограничимся дискообразной формой кавернообразующего эле­мента. Логично допустить, что нормальная сила, действующая на диск при малых и умеренных углах атаки (до 50°), следует за­кону косинуса. Итак, приближенно

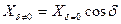, (7.117)

и далее

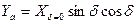; (7.118)

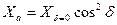. (7.119)

Принятая гипотеза хорошо согласуется с экспериментом (до δ~ 50°) и может быть распространена на кавернообразующие элементы другой конфигурации, нежели диск.

Импульсу поперечной силы, развиваемой на кавернообразующем элементе, должно соответствовать изменение количества дви­жения в следе, равное по величине и противоположное по нап­равлению. Это означает, что при подъемной силе ось каверны должна отклоняться вниз, а при топящей силе должен наблю­даться скос оси каверны вверх.

Наглядную картину течения при угле атаки легко получить, если заменить насадок П-образным вихрем. Направление враще­ния вихрей определяют знаком скоса оси каверны.

В скошенном потоке должны деформироваться и поперечные сечения каверны. Миделево сечение уменьшается. Это следует из принятого закона изменения сопротивления (7.119) и инте­грального соотношения (7.73). Сопоставляя эти формулы, най­дем

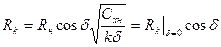. (7.120)

Как видим, при угле атаки δ кавитатора средний радиус миделевого сечения уменьшается пропорционально соsδ. По-ви­димому такое же положение будет соблюдаться и в срединной домидельной части каверны, т. е. приближенно можно положить

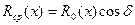, (7.121)

где R₀(х) — радиус осесимметричной невозмущенной каверны. Вместе с тем проекция наклонного диска на вертикальную плос­кость будет эллипсоидальной. Поэтому можно ожидать, что и по­перечные сечения каверны в домидельной части будут характери­зоваться эллипсами. Опыты Цейтлина подтвердили это, дав следующую зависимость для отношения полуосей эллипса:

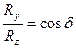. (7.122)

Сопоставляя (7.121) и (7.122), окончательно найдем

, .

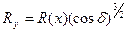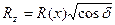Обратим внимание, что в непосредственной близости от кави­татора полученные соотношения теряют достоверность. В самом деле полуоси эллипса в плоскости диска при нулевом угле атаки равны 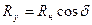, 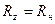и поэтому 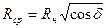, т. е. сред­ний радиус сечения больше, чем предсказываемый формулой (7.121). Для устранения противоречия нужно вводить корректирующую функцию.