При достаточно малых числах кавитации основной участок каверны должен представлять собой удлиненное тело вращения. В самом деле, согласно (7.61), 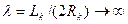 при
при 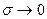 . Поскольку крутой поворот потока завершается на начальном участке, на основном участке должны выполняться условия
. Поскольку крутой поворот потока завершается на начальном участке, на основном участке должны выполняться условия 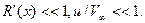 Эти условия дают возможность различными путями с различной степенью точности вывести приближенные уравнения, управляющие конфигурацией каверны.
Эти условия дают возможность различными путями с различной степенью точности вывести приближенные уравнения, управляющие конфигурацией каверны.
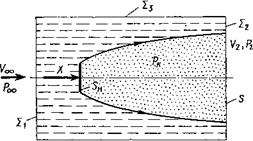
Воспользуемся сначала интегральной формой теоремы импульсов. С этой целью выделим контрольный объем жидкости цилиндрической поверхностью Σ3, ось которой совпадает с осью симметрии кавернообразующего тела и каверны, и двумя плоскостями, перпендикулярными оси симметрии. Одну плоскость Σ1 расположим далеко вверх по потоку так, чтобы скорость жидкости в ней была постоянной и равной невозмущенной скорости набегающего потока V∞. Вторую плоскость Σ2 проведем через произвольную точку продольной оси в пределах домиделевой части каверны. Эта плоскость создает сечение каверны радиусом R и площадью 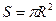 . Цилиндрическая поверхность Σ3 охватывает кавернообразующее тело и каверну (рис. 7.13).
. Цилиндрическая поверхность Σ3 охватывает кавернообразующее тело и каверну (рис. 7.13).
|
Рис. 7.13
Теорема о количестве движения: изменение количества движения жидкости в единицу времени равно импульсу давлений и внешних сил, действующих на рассматриваемый объём.
Запишем теперь теорему о количестве движения для выделенного контрольного объема жидкости в проекции на ось x:
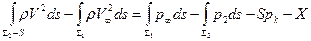 . (7.66)
. (7.66)
Здесь 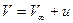 , X- сила кавитационного сопротивления. Интегралы по Σ3 отсутствуют, так как радиус цилиндрической поверхности можно устремить в бесконечность, где возмущенная радиальная скорость v стремится к нулю как 1/r3 (течение от диполя). Интеграл по Σ3 от давления
, X- сила кавитационного сопротивления. Интегралы по Σ3 отсутствуют, так как радиус цилиндрической поверхности можно устремить в бесконечность, где возмущенная радиальная скорость v стремится к нулю как 1/r3 (течение от диполя). Интеграл по Σ3 от давления 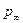 также даст нуль.
также даст нуль.
Упростим это выражение. Из уравнения Бернулли выразим давление 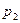 :
:
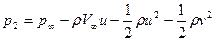 (7.67)
(7.67)
Тогда сопротивление равно
 (7.68)
(7.68)
Для вычисления первого слагаемого используем закон сохранения массы, выраженный в форме уравнения расхода:
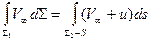 (7.69)
(7.69)
Отсюда следует, что
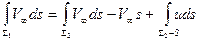
Поэтому
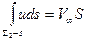 (7.70)
(7.70)
Используя этот результат и (7.68), запишем основное интегральное соотношение теоремы импульсов для кавитационных течений:
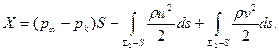 (7.71)
(7.71)
Поделив обе части равенства на скоростной напор 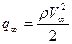 и на площадь кавернообразующего тела (насадка) Sн перейдём к безразмерной форме интегрального соотношения:
и на площадь кавернообразующего тела (насадка) Sн перейдём к безразмерной форме интегрального соотношения:
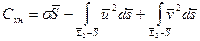 , (7.72)
, (7.72)
где тильдой отмечены безразмерные величины:
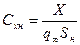 ,
, 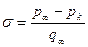 ,
, 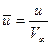
 ,
,
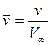 ,
, 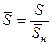 .
.
Полученное уравнение весьма удобно для приближенного анализа. В условиях 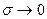 справедливо u<<v. Следовательно, вторым интегралом можно пренебречь. Далее проведём контрольную плоскость Σ2 в миделевом сечении, так что v=0. Поэтому
справедливо u<<v. Следовательно, вторым интегралом можно пренебречь. Далее проведём контрольную плоскость Σ2 в миделевом сечении, так что v=0. Поэтому
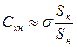 . (7.73)
. (7.73)
Если в коэффициенте сопротивления 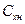 перейти к площади сравнения
перейти к площади сравнения 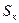 (площади миделя каверны) и ввести новый коэффициент сопротивления
(площади миделя каверны) и ввести новый коэффициент сопротивления 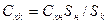 , то окажется
, то окажется
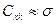 . (7.74)
. (7.74)
В действительности 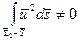 и в последнюю формулу можно ввести поправочный коэффициент k:
и в последнюю формулу можно ввести поправочный коэффициент k:
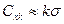 . (7.75)
. (7.75)
Из (7.73) непосредственно следует, что максимальный радиус равен
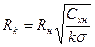 .
.
Экспериментально доказано, что поправочный множитель k является слабой функцией от числа кавитации и при малых значениях σ его значение близко к единице (k =0,95…1,0).
Основное интегральное соотношение (7.71) может быть использовано и для нахождения радиуса каверны в произвольном сечении, а не только в миделевом. В самом деле, пренебрегая величиной интеграла  , получим
, получим
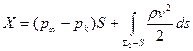 . (7.76)
. (7.76)
В плоскости Σ2 течение теперь может рассматриваться как чисто радиальное. На поверхности каверны поток должен быть тангенциальным, т.е. должно быть
 , (7.77)
, (7.77)
или в линейном приближении
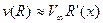 . (7.78)
. (7.78)
Иными словами, в плоскости Σ2 должно наблюдаться радиальное течение жидкости, вызванное расширением парогазовой круговой полости, обладающей скоростью стенок v(R). Радиальная скорость такого течения на произвольном радиусе r может быть найдена из равенства расходов жидкости через две окружности: радиуса R и радиуса r. Это дает соотношение:
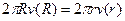 ,
,
а с учётом (7.77)
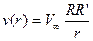 (7.79)
(7.79)
Рассмотрим теперь интеграл
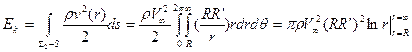 . (7.80)
. (7.80)
Как видим, при подстановке верхнего предела значение интеграла стремится к бесконечности, т.е. для радиального расширения круговой каверны в плоской задаче требуется бесконечное приращение кинетической энергии. Это противоречит физической сущности задачи. Поэтому для получения практических результатов будем считать, что внешний радиус границы течения в плоскости Σ2 имеет большое, но конечное значение R*(x), которое можно уточнить после согласования с экспериментальными данными или результатами более строгих теоретических анализов (рис. 7.14).
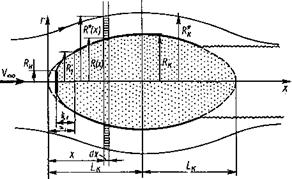
Рис. 7.14
Сделанное допущение означает, что все возмущения в движении жидкости, вызванные присутствием кавернообразующего тела и каверны, сосредоточены в жидком кольце с внутренним радиусом R(x) и внешним радиусом R*(x). За пределами внешнего радиуса этого кольца возмущения равны нулю. Этот образ радиально расширяющегося жидкого кольца и дал наименование данному подходу: метод жидкого кольцевого слоя.
Введём обозначение:
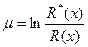 (7.81)
(7.81)
В срединной части каверны R(x) изменяется слабо и поэтому справедливо положить 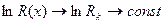 . Аналогичное заключение можно сделать и относительно внешнего радиуса жидкого кольца
. Аналогичное заключение можно сделать и относительно внешнего радиуса жидкого кольца  . И тогда
. И тогда
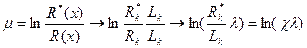 , (7.82)
, (7.82)
где 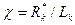 - некоторый множитель, представляющий собой отношение внешнего радиуса жидкого кольца в миделевом сечении к полудлине каверны; λ=Lk/Rk – удлинение каверны.
- некоторый множитель, представляющий собой отношение внешнего радиуса жидкого кольца в миделевом сечении к полудлине каверны; λ=Lk/Rk – удлинение каверны.
Из экспериментов получено χ=0,54…0,64. Причём большое значение целесообразнее применять при σ=0,06, а меньшее - при σ=0…0,03. Теоретическая оценка величины χ равна 0,605.
Функцию μ часто трактуют как меру инерциальных свойств жидкого кольца.
Вернёмся к интегральному соотношение (7.76) можно переписать в виде:
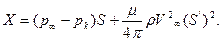 (7.83)
(7.83)
Прейдем в данном уравнении от независимой переменной х к независимой переменной S согласно соотношениям

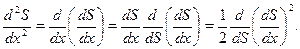
Продифференцируем (7.83) по S. Получаем каноническую форму дифференциального уравнения для приближенного определения профиля каверны при малых числах кавитации:
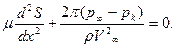 (7.84)
(7.84)
Интегрирование дает
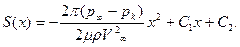 (7.85)
(7.85)
При граничных условиях S=Sk, S’=0, при x=0 получаем C1=0,C2=Sk .
Следовательно,
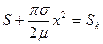 (7.86)
(7.86)
или получаем каноническое уравнение эллипсоида:
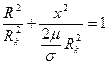 . (7.87)
. (7.87)
с полуосями:
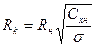 (7.88)
(7.88)
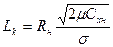 (7.89)
(7.89)
Для построения в дальнейшем профиля составной каверны начало координат эллипсоидной каверны удобнее разместить в носике эллипсоида. Тогда при x=0 будем иметь S=0,из (7.83) получим условие
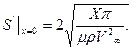 (7.90)
(7.90)
В новых координатах 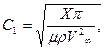 С2=0, а уравнение профиля каверны запишем в виде:
С2=0, а уравнение профиля каверны запишем в виде:
 (7.91)
(7.91)
или
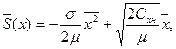 (7.92)
(7.92)
где
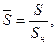
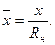
Если использовать значение полуосей, то можно дать альтернативную формулу для закона изменения радиуса эллипсоидальной каверны:
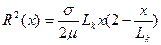 (7.93)
(7.93)
Удлинение каверны равно
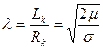 (7.94)
(7.94)
Удлинение эллипсоидальной каверны. Расчёт μ
Используя определение μ, получаем
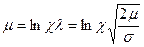 (7.95)
(7.95)
Таким образом, для нахождения μ необходимо решать трансцендентное уравнение. Это решение можно осуществить численно методом последовательных приближений:
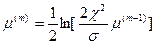 ,
, 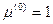 , (7.96)
, (7.96)
m- номер итерации.
В диапазоне чисел кавитации σ=0,06…0,02 параметр μ изменяется в пределах 1,5…2,0. этому же диапазону σ соответствуют удлинения λ=7…13.
Профиль каверны на основном участке в упрощенном виде:
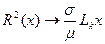 . (7.97)
. (7.97)
Если принять, что в сечении сращивание х1 радиус каверны R1=2Rн, то
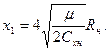 (7.98)
(7.98)
При малых числах кавитации х1~4Rн.
Полудлина составной каверны определится как:
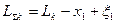 , (7.99)
, (7.99)
т.е. она будет несколько меньше, чем полудлина эллипсоидальной каверны. Анализ слагаемых, входящих в последнюю формулу, позволяет составить зависимость вида
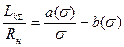 , (7.100)
, (7.100)
где функции 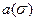 и
и 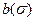 слабо зависят от числа кавитации. Эксперименты с диском легли в основу эмпирической формулы
слабо зависят от числа кавитации. Эксперименты с диском легли в основу эмпирической формулы
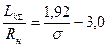 (7.101)
(7.101)
 2014-02-02
2014-02-02 598
598








