Коэффициент расхода газа

Количество газа, потребное для создания и поддержания искусственного кавитационного течения, характеризуется безразмерным коэффициентом расхода:

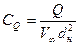, (7.126)

где Q — объемный расход газа поддува, приведенный к давлению в каверне, [ м³/с ]; d_н — диаметр насадка, [ м ]; 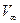— скорость набегаю­щего потока, [ м/с ].

Возможны два режима уноса газа: по продольным вихрям и в виде периодически отрывающихся порций. Порции иногда прини­мают тороидальный вид и поэтому второй режим уноса газа на­зывают уносом по кольцевым вихрям.

С помощью теории размерностей можно записать

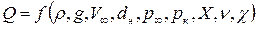(7.127)

и далее

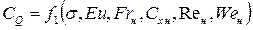, (7.128)

где приняты стандартные определения критериев подобия. Индекс «н» означает, что в качестве линейного размера принят диаметр кавитатора.

Числа Рейнольдса и Вебера практически не поддаются регулированию при проведении эксперимента. Их влияние пока изучено недостаточно полно. Поэтому для простоты анализа выбросим их из рассмотрения. В соотношении (7.128)отброшено влияние свободной поверхности, которое можно было бы отразить глубиной по­гружения кавитатора. Итак,

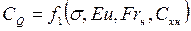. (7.129)

Первый режим уноса газа наблюдается только при искусствен­ной кавитации и характерен для режимов сильного влияния весомости (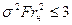). При Fr = const продольные вихри образуются при меньших числах кавитации. Второй режим существует при более высоких числах кавитации. Он характеризуется большой нестационарностью. Каверна периодически заполняется пеной. За­тем под воздействием возвратной струйки от каверны отрываются крупные газожидкостные образования. Каверна восстанавливает свои размеры, и далее процесс разрушения каверны повторяется.

Создать единую теорию уноса газа из каверны, которая позво­ляла бы рассчитывать на всех режимах течения, не удается. Приближенной оценке поддаются отдельные режимы течения.

Более простым для анализа оказывается случай уноса газа по продольным вихрям, характерный для малых чисел Фруда и соответственно больших чисел Эйлера.

Теория Эпштейна. Предположим, что по мере движения тела образуются все новые участки вихревых трубок. Давление в каверне и в трубах одинаково. Поэтому газ покоится относительно частиц жидкости. Пусть скорость образования трубок равна скоро­сти набегающего потока, тогда объемный расход газа в вихревых трубках будет равен

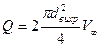(7.130)

или в безразмерной форме

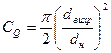. (7.131)

Выразим квадрат отношения диаметра вихревых трубок 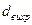к диаметру кавитатора 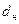из уравнения Бернулли. При этом уч­тем, что расстояние между вихрями «b» много больше, чем диаметр вихрей. Пусть h - высота всплывания конца каверны, которая определяется формулой (7.116). Тогда

,

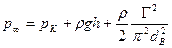и далее

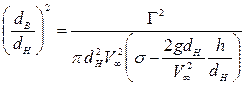. (7.132)

Вспоминая теперь значение для Г (7.111), получим

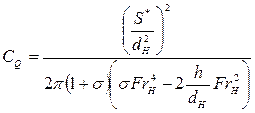. (7.133)

Здесь S* —площадь вертикальной проекции каверны. Примем ее равной площади эллипса, соответствующего каверне в невесомой жидкости, а значение h получим из (7. 112).Тогда получается окончательная формула Эпштейна:

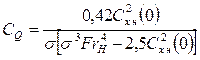. (7.134)

Нетрудно заметить, что если ввести вместо d_H новый характерный линейный размер 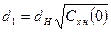,то C_Q не будет зависеть от 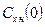. Обобщенная экспериментальная кривая подобного типа при фиксированном значении числа Fr_H для семейства конусов с угла­ми раствора 2=30°... 180° приведена на рис. 7.18. Как видим,

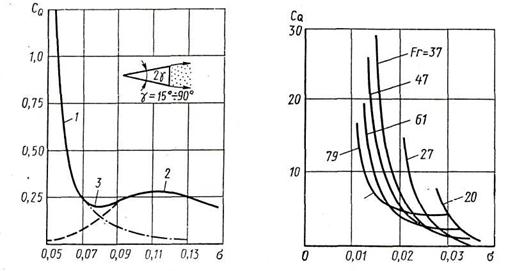
Рис. 7.18 Рис. 7.19

существуют оба типа уноса газа. Левая ветвь кривой 1 соответствует уносу газа по продольным вихрям, правая ветвь 2— по коль­цевым вихрям, средняя часть 3 отвечает промежуточному режиму, при котором могут иногда наблюдаться обе формы уноса газа од­новременно. Левая ветвь 1 хорошо описывается формулой (7.134). Семейство экспериментальных кривых 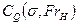на рис. 7.19 дает представление о влиянии больших чисел Фруда на коэффициент расхода газа поддува при кавитационном обтека­нии диска.

Формула Эпштейна не отражает влияния числа Эйлера. Между тем ясно, что при малых числах Эйлера Eu=p_∞/ρV_∞²/2, со­поставимых с числом естественной кавитации σ_υ=(p_∞-p_υ)ρV_∞²/2, вентилируемая каверна будет мало отличаться от естественной, а коэффициент расхода газа поддува будет стремиться к нулю. С учетом этого соображения предложена другая формула для расчета расхода газа поддува:

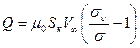, (7.135)

где Q —объемный расход, отнесенный к давлению окружающей среды; 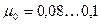- коэффициент, определенный эксперимен­тальным путем.

Последней формуле можно придать иной вид:

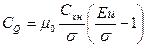, (7.136)

так как .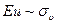

Из формулы (7. 133) видно, что 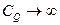, если знаменатель стремится к нулю. При фиксированном числе Фруда это дости­гается при некотором минимальном числе кавитации

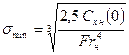. (7.137)

В случае диска

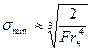. (7.138)

Отсюда следует вывод, что никакое увеличение расхода газа не дает уменьшения числа кавитации ниже некоторого минималь­ного значения.

Рис. 7.20

На некоторых режимах стенки каверны приобретают волнообразные деформации и тогда говорят о пульсирующих кавернах (рис. 7.20). На длине каверны может располагаться одна, две … пять волн. Иногда каверна теряет общую устойчивость и она скачкообразно меняет свой объем (порционный отрыв каверны).