Физическое моделирование процесса погружения

В отличие от рассмотренного ранее примера о подобии течений при проникании клина и конуса в жидкость рассмотрим теперь условие подобия полного процесса погружения тела с характерным линейный размером L, массой m и моментом инерции J. Пусть кинематиче­ские условия входа характеризуются скоростью приводнения V₀, углом атаки α и углом приводнения θ. Физические параметры га­зовой среды сопроводим индексом «г», а жидкости — индексом «ж». Тогда в предположении несжимаемости жидкости будем иметь сле­дующие размерные величины, характеризующие процесс: ρ_г — плотность, p_г — давление, Т_г —температура, υ_г —коэффициент ки­нематический вязкости, k_г — показатель адиабаты, ρ_ж — плотность, υ_ж — коэффициент кинематической вязкости, χ — коэффициент по­верхностного натчженич, Т_ж — температура, g — ускорение свобод­ного падения. Общее число параметров, определяющих процесс погружения, равно 16. Согласно теории подобия можно сформировать 13 безразмерных комплексов. Выпишем их:

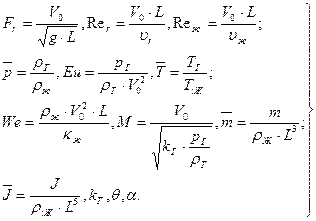(8.1)

Некоторые из указанных параметров в определенных условиях экспериментов играют незначительную роль и могут быть отброшены при моделировании. Так, очевидно, что силы вязкостной природы в жидкости в начальный период погружения не могут оказать заметного влияния на величину нагрузок, так как погра­ничный слой не успевает развиться. На режиме развитой кавита­ции эти силы также невелики. Отсюда следует, что подобием по числу Rе_ж можно пренебречь. Кривизна свободной поверхности жидкости на большей площади мала, вследствие чего действие сил поверхностного натяжения может проявиться лишь в брызговых струях и в процессах их разрушения (каплеобразование). Поэтому подобие по числу We можно опустить. Силы вязкостной природы в газовой атмосфере, характеризуемые числом Re_г, существенно меньше сил ударной природы в процессе погружения и могут быть отброшены без заметной потери точности.

Оставляя в конечном счете лишь важнейшие физические факторы, т. е. осуществляя частичное моделирование процесса погруже­ния с кавернообразованием, приходим к необходимости соблюдать подобие по значительно меньшему числу критериев, нежели их указано в (8.1), а именно: Fr, 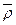, Eu, 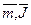, M, θ, α.

Рассмотрим случаи малых чисел М (M<<1) и два принципиаль­но разных подхода к одновременному удовлетворению правых трех указанных критериев:

, , .

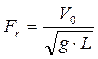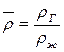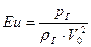В одном из них соблюдение равенства числа Фруда при умень­шенном размере модели достигается снижением скорости входа V₀. При неизменной атмосфере это должно привести к росту числа Эйлера. Снижение давления не даст желаемого эффекта, так как пропорционально снизится и плотность газа. Поэтому в качестве газовой атмосферы необходимо применять газ с более высокой плотностью.