2014-02-02
1997
Особенности составления матричных уравнений при наличии индуктивных связей и ветвей с идеальными источниками
Лекция N 12
Как было показано ранее (см. лекцию N 6), для схем, не содержащих индуктивно связанные элементы, матрицы сопротивлений и проводимостей ветвей являются диагональными, т.е. все их элементы, за исключением стоящих на главной диагонали, равны нулю.
В общем случае разветвленной цепи со взаимной индукцией матрица сопротивлений ветвей имеет вид
Z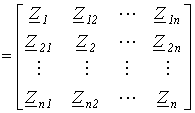 
.
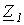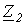Здесь элементы главной диагонали 
, 
,… 
- комплексные сопротивления ветвей схемы; элементы вне главной диагонали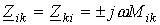 
- комплексные сопротивления индуктивной связи i- й и k – й ветвей (знак “+” ставится при одинаковой ориентации ветвей относительно одноименных зажимов, в противном случае ставится знак “-”).
Матрица проводимостей ветвей в цепях со взаимной индукцией определяется согласно
Y = Z –1.
Зная матрицы и Y, можно составить контурные уравнения, а также узловые, т.е. в матричной форме метод узловых потенциалов распространяется на анализ цепей с индуктивно связанными элементами.
Следует отметить, что обычно не все ветви схемы индуктивно связаны между собой. В этом случае с помощью соответствующей нумерации ветвей графа матрице Z целесообразно придать квазидиагональную форму
Z 
,
что облегчает ее обращение, поскольку
Y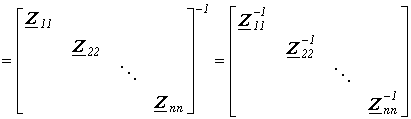 
,
где подматрицы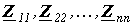 
могут быть квадратными диагональными или недиагональными.
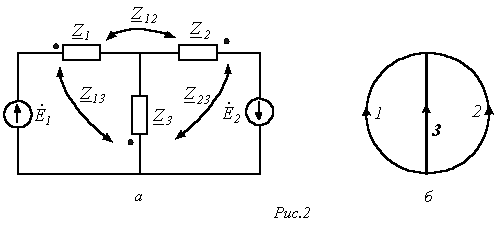
В качестве примера составим матрицы Z и Y для схемы на рис. 1,а, граф которой приведен на рис. 1,б.
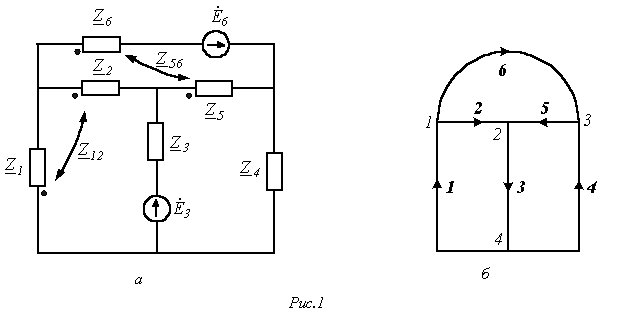
Для принятой нумерации ветвей матрица сопротивлений ветвей
Z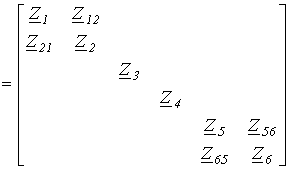 
.
В этой матрице можно выделить три подматрицы, обращая которые, получим
| Z-111 |  ; |
| Z-122 |  ; |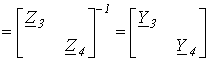
| Z-133 |  . |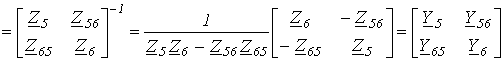
Таким образом, матрица проводимостей ветвей
Y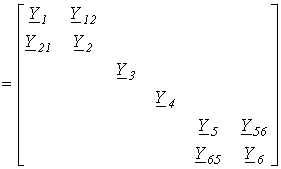 
.
Отметим, что при принятой ориентации ветве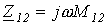й 
и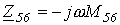 
.
 |
В качестве примера матричного расчета цепей с индуктивными связями запишем контурные уравнения в матричной форме для цепи рис. 2,а.
