2014-02-02
487
Переход от изображения искомой величины к оригиналу может быть осуществлен следующими способами:
1. Посредством обратного преобразования Лапласа
,
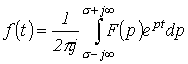которое представляет собой решение интегрального уравнения (1) и сокращенно записывается, как:
.
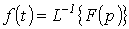На практике этот способ применяется редко.
2. По таблицам соответствия между оригиналами и изображениями
В специальной литературе имеется достаточно большое число формул соответствия, охватывающих практически все задачи электротехники. Согласно данному способу необходимо получить изображение искомой величины в виде, соответствующем табличному, после чего выписать из таблицы выражение оригинала.
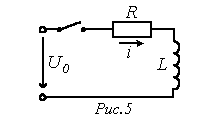Например, для изображения тока в цепи на рис. 5 можно записать
.
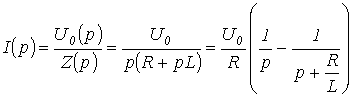Тогда в соответствии с данными табл. 1
,
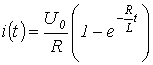что соответствует известному результату.
3. С использованием формулы разложения
Пусть изображение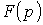 
искомой переменной определяется отношением двух полиномов
,
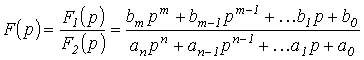где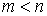 
.
Это выражение может быть представлено в виде суммы простых дробей
 ,
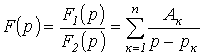| (3) |
где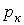 
- к-й корень уравнения 
.
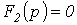Для определения коэффициентов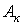 
умножим левую и правую части соотношения (3) на (
):
.
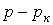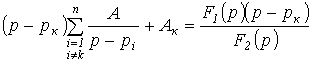При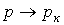 
.
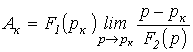Рассматривая полученную неопределенность типа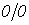 
по правилу Лапиталя, запишем
.
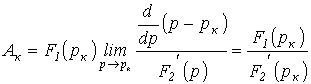Таким образом,
.
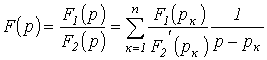Поскольку отношение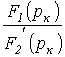 
есть постоянный коэффициент, то учитывая, что 
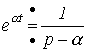, окончательно получаем
 .
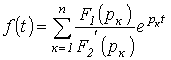| (4) |
Соотношение (4) представляет собой формулу разложения. Если один из корней уравнения 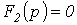равен нулю, т.е. 
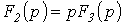, то уравнение (4) сводится к виду
.
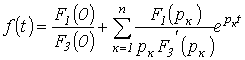В заключение раздела отметим, что для нахождения начального 
и конечного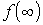 
значений оригинала можно использовать предельные соотношения
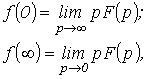
которые также могут служить для оценки правильности полученного изображения.
