Аналитическая запись

Произведение булевых переменных называется булевым произведением. Булево произведение называется элементарным, если переменные в него входят только один раз в прямой или инверсной форме.

Пример. 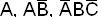- элементарные произведения, 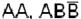- эти произведения не являются элементарными.

Число переменных, образующих элементарное произведение, называется длиной или рангом элементарного произведения.

Пример. 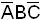- ранг 3.

Минтермом или конституентой единицы n переменных называется элементарное произведение ранга n.

Аналогичные определения существует и для булевых сумм.

Пример. 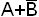- элементарная сумма ранга 2; 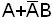не является элементарной суммой.

Макстермом или конституентой нуля n переменных называется элементарная булева сумма ранга n.

Как булева функция минтерм принимает значение единицы только на одном наборе, аналогично макстерм принимает только на одном наборе значение нуля.

При записи минтерма часто используется буква m с индексом того набора, на котором данный минтерм принимает значение единицы.

Пример. =m₅.

Двоичный эквивалент индекса для минтерма может быть определен из записи минтерма подстановкой вместо прямых форм переменных цифры 1, а вместо инверсных – цифры 0.

Пример. 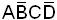- минтерм ранга 4;

1010 – двоичный эквивалент индекса.

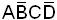= m₁₀.

При этом не следует забывать, что при переходе от индексной записи минтерма к аналитической следует восстановить все переменные, входящие в данную запись.

Пример. m₅ – ранга 4 имеет запись 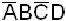; m₅ – ранга 3 имеет запись .

Аналогично при записи макстерма используется буква М с индексом, двоичная запись которого содержит 1, если соответствующая переменная входит в аналитическую запись макстерма в прямой форме, и 0, если в инверсной.

Пример. 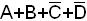=М₁₁₀₀= М₁₂.

Между минтермами и макстермами существует следующая связь:

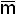_i = M₂ⁿ_-i-1; 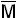_i = m₂ⁿ_-i-1.

Булева сумма всех минтермов ранга n равна единице:

2ⁿ-1

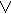m_i =1.

i=0

Это следует из того, что число различных минтермов ранга n равно 2ⁿ, т.е. числу различных наборов n переменных, а функция, принимающая на всех наборах значение 1, есть константа 1.

Используя теорему де Моргана, можно показать, что произведение всех макстермов ранга n равно нулю:

2ⁿ-1

Λ M_i =0.

i=0

Из этих уравнений следует

m_im_j =0 при i≠j;

M_i + M_j =1 при i≠j.

Равенства очевидны, если вспомнить, что минтерм – это конституента единицы, а макстерм – конституента нуля.