Любая булева функция может быть выражена булевой суммой минтермов или произведением макстермов.
Таблица 8. Составим таблицу функций и найдем булево



 A B C f(ABC) выражение для данной функции. Из табл.8 видно,
A B C f(ABC) выражение для данной функции. Из табл.8 видно,
 0 0 0 0= α0 что функция равна единице, только на наборах,
0 0 0 0= α0 что функция равна единице, только на наборах,
0 0 1 1= α1 равных 001, 101, 111, что соответствует минтер-
0 1 0 0= α2 мам 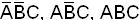 .
.
0 1 1 0= α3 Это значит, что данная функция может быть
1 0 0 0= α4 дизъюнкцией этих минтермов, т.е.
1 0 1 1= α5 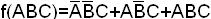 = m1 + m5+ m7.
= m1 + m5+ m7.
1 1 0 0= α6 Чтобы убедиться в сказанном, запишем дан-
1 1 1 1= α7 ную функцию в виде суммы произведений значений функции на соответствующие минтермы:
f(ABC)= α0 m0 + α1 m1 + α2 m2 + α3 m3 + α4 m4 + α5 m5 + α6 m6 + α7 m7 =
= 0m0 + 1m1 + 0m2 + 0m3 + 0m4 + 1m5 + 0m6 + 1m7,
где αi – значение данной функции на i –ом наборе.
Следовательно, справедлива запись:
2n-1
f(x1 x2 … xn)= 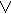 α i mi.
α i mi.
i=0
Применив формулу де Моргана, найдем выражение
2n-1
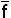 (x1 x2 … xn)=
(x1 x2 … xn)= 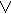
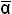 i mi.
i mi.
i=0
 2n-1 2n-1 2n-1 2n-1
2n-1 2n-1 2n-1 2n-1
 f(x1 x2 … xn)=
f(x1 x2 … xn)= 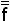 (x1 x2 … xn)=
(x1 x2 … xn)= 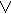
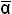 i mi = Λ (
i mi = Λ (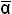 i mi)= Λ (α i +
i mi)= Λ (α i + 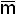 i)= Λ (α i +M2n-i-1).
i)= Λ (α i +M2n-i-1).
i=0 i=0 i=0 i=0
Основная теорема:
2n-1 2n-1
f(x1 x2 … xn)= 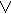 α i mi = Λ (α i +M2n-i-1).
α i mi = Λ (α i +M2n-i-1).
i=0 i=0
Для аналитических записей булевых функций существуют следующие определения:
Булева сумма элементарных произведений называется дизъюнктивной нормальной формой (ДНФ).
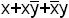 - ДНФ;
- ДНФ;
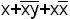 - не является ДНФ.
- не является ДНФ.
Булево произведение элементарных сумм называется конъюнктивной нормальной формой (КНФ).
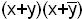 - КНФ;
- КНФ;
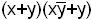 -не является КНФ.
-не является КНФ.
ДНФ функции n переменных, состоящая из элементарных произведений ранга n (т.е. из минтермов), называется совершенной дизъюнктивной нормальной формой функции (СДНФ).
КНФ функции n переменных, состоящая из элементарных сумм ранга n (т.е. из макстермов), называется совершенной конъюнктивной нормальной формой функции (СКНФ).
Основная теорема содержит запись СДНФ и СКНФ функций.
Из теоремы следует, что запись СДНФ (или СКНФ) булевой функции единственна.
 2014-02-02
2014-02-02 774
774








