Сокращенные, тупиковые и минимальные формы булевых функций

ДНФ (КНФ) называется минимальной, если количество букв, которые она содержит, будет не больше, чем в любой другой ДНФ (КНФ) той же функции.

Пусть на каком-то наборе аргументов функция f₁(x₁ x₂ … x_n) принимает значение α₁, а функция f₂(x₁ x₂ … x_n) - значения α₂. Тогда говорят, что функция f₁ на данном наборе накрывает значение α₂ функции f₂ своим значением α₁.

Аналогично можно сказать, что функция f₂ на данном наборе накрывает значение α₁ функции f₁ своим значением α₂.

Пример. f₁₁(xy)= m₀+m₁+m₃.

Каждый минтерм накрывает своим значением единица на соответствующем наборе единичное значение функции f₁₁, а все минтермы, входящие в СДНФ функции, накрывают значениями единица все единицы функции.

Определение. Если некоторая булева функция [V1] φ равна нулю на тех же наборах, на которых равна нулю другая функция f, то говорят, что функция φ входит в функцию f:

.

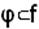Таким образом, функция φ накрывает нулями все нули функции f и, следовательно, имеет не меньше нулей, чем функция f.

Пример.

а) Любой минтерм СДНФ функции f входит в f; f₆(xy)= m₁+m₂ и равна 0 на наборах <00>, <11>

f₀(xy) f₆(xy);

f₄(xy) f₆(xy);

f₂(xy) f₆(xy);

б) Функция f₀=0 – входит в любую булеву функцию.

в) В функцию

- входят все функции n переменных.

Определение. Функция φ, входящая в данную функцию f, называется ее импликантой.

Собственной частью конъюнкции называется конъюнкция, полученная из данной конъюнкции путем исключения одного или нескольких сомножителей.

Простыми импликантами булевой функции называются такие элементарные конъюнкции, которые сами входят в данную функцию, но никакая собственная часть этих конъюнкций в эту функцию не входит.

Пример. 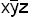имеет собственные части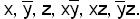

Пример. Пусть выполняется условие

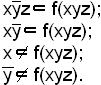
Значит, 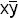- простая импликанта функции f(xyz).

Пример. Рассмотрим функцию, представленную в табл.16.

Таблица 16

x 0 0 0 0 1 1 1 1

y 0 0 1 1 0 0 1 1

z 0 1 0 1 0 1 0 1

f(xzy) 0 0 0 0 1 0 1 1

xyz 0 0 0 0 0 0 0 1

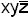0 0 0 0 0 0 1 0

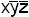0 0 0 0 1 0 0 0

xy 0 0 0 0 0 0 1 1

В эту функцию входят xyz, 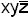, , 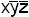xy, так как они равны нулю на всех наборах, где f(xyz)=0, но простыми импликантами будут 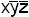и xy.

Теорема. Любая булева функция равна дизъюнкции всех своих простых импликант.

Доказательство. Так как все простые импликанты входят в данную функцию (по определению), то они равны нулю на всех наборах, на которых функция равна нулю. Следовательно, и дизъюнкция их равна нулю на тех наборах, где равна нулю функция.

Так как СДНФ функции есть дизъюнкция элементарных конъюнкций, а простые импликанты есть собственные части этих конъюнкций, то на тех наборах, где СДНФ функции равна 1, обязательно равна единице и одна из простых импликант. Таким образом, дизъюнкция простых импликант принимает значения 1 на тех же наборах, что и сама функция.

Теорема доказана.

Дизъюнкция всех простых импликант называется сокращенной ДНФ функции. Любая переключательная функция имеет единственную сокращенную ДНФ.