Рассмотрим графический метод отыскания тупиковых форм функции из сокращенной ДНФ.
Импликантная матрица представляет собой таблицу, столбцы которой соответствуют всем конституентам единицы СДНФ заданной функции, а строки – всем простым импликантам.
В таблице по строке каждой импликанты отмечаются те минтермы, которые ею поглощаются.
Чтобы получить минимальную ДНФ заданной функции, достаточно найти минимальное число импликант, которые совместно накрывают все столбы импликантной матрицы, если в каком-либо из столбцов составленной импликантной матрицы функции имеется только одна отметка, то соответствующая ей импликанта является обязательной и обязательно входит в тупиковую форму функции, так как без нее будет получено накрытие всего множества минтермов.
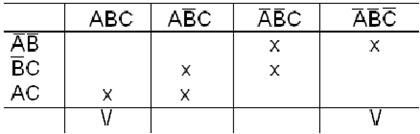
Для случая  имеем импликантную матрицу, представленную в табл.18.
имеем импликантную матрицу, представленную в табл.18.
В данном случае импликанты AC и 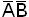 являются обязательными. Их сумма покрывает все минтермы, следовательно, тупиковая форма
являются обязательными. Их сумма покрывает все минтермы, следовательно, тупиковая форма 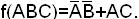 Она единственна и поэтому является минимальной.
Она единственна и поэтому является минимальной.
Таблица 18.
Пример. Найти минимальную ДНФ функции, используя метод Квайна и метод импликантных матриц:


Сокращенная ДНФ
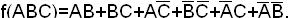
Импликантная матрица функции дана в табл.19.
Таблица 19
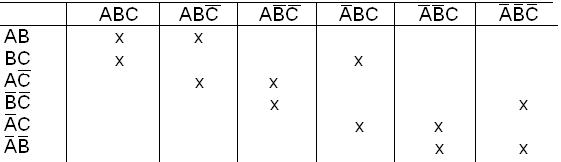
Так как нет столбцов с одной отметкой, то ни одна из импликант не является обязательной. Найдем минимальное количество простых импликант, накрывающее все колонки.
Возможны две тупиковые формы функции:
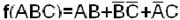 ;
;
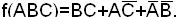
Обе формы содержат одинаковое число букв и, следовательно, обе являются минимальными.
Возможны другие тупиковые формы данной функции, но они не минимальны:
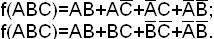
 2014-02-02
2014-02-02 4930
4930








