Температура 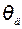в плоскости сдвига

Температуру , которую стружка приобретает в результате деформации металла в плоскости сдвига найдём из уравнения баланса тепловых потоков.

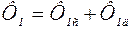(2.12)

Общая мощность первого источника тепла равна

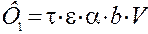, (2.13)

где 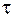– средние касательные напряжения в плоскости сдвига.

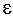– относительный (истинный) сдвиг.

abV – объём металла, переходящий в стружку в единицу времени.

Тепловой поток Ф_1с, отводящий равномерно прогретой до температуры 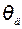стружки будет равен

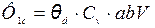(2.14)

где 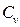– коэффициент объёмной теплоёмкости обрабатываемого материала.

Тепловой поток 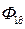_, поступающий от плоскости сдвига в деталь, пренебрежимо мал при достаточно больших (>10) значениях критерия Пекле, и его мы не будем учитывать.

(2.15)

Подставляя (2.19) и (2.20) в (2.18), получим

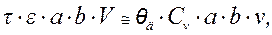
откуда ,

или 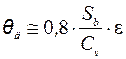, (2.16)

где S_в – действительный предел прочности обрабатываемого материала при растяжении .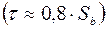

Относительный (истинный) сдвиг определяется следующим образом

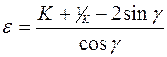(2.17)

где K – коэффициент усадки стружки;

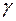– главный передний угол.

Из формулы (2.16) следует, что температура в плоскости сдвига зависит от прочностных и теплофизических характеристик обрабатываемого материала

(S_в и C_v), а также от относительного (истинного) сдвига .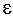

Температура на передней поверхности инструмента 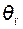определяется следующим выражением

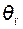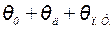= (2.18)

где 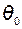– начальная температура заготовки ,

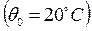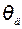– температура в плоскости сдвига;

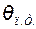– температура передней поверхности от трения стружки.