Методы решения краевых задач теплопроводности

В настоящее время разработано множество методов решения дифференциального уравнения теплопроводности: аналитические, численные и методы математического моделирования.

Решение дифференциального уравнения теплопроводности при использовании аналитических методов получается в виде формулы, а для численных методов − в виде массива чисел.

Достоинство аналитических методов: обозримость получаемых результатов, возможность полного анализа полученного решения. Недостаток аналитических методов: возможность получения решения, как правило, для областей канонической формы. Для декартовой системы координат область канонической формы ограничивается линиями, параллельными осям OX и OY.

Достоинство численных методов: возможность решать сложные задачи, недоступные для аналитических методов. Массив чисел, полученных численными методами, обычно представляется в табличной форме или аппроксимируется формулой для последующего анализа.

Аналитические и численные методы следует рассматривать как дополняющие друг друга, а не как конкурирующие.

Для решения задач теплофизики резания наибольшее распространение получили следующие аналитические методы: метод точечных источников и метод быстродвижущихся источников тепла. Рассмотрим их по порядку.

Решением дифференциального уравнения теплопроводности (1.15) является функция 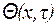, которая при подстановке в уравнение (1.15) обращает его в тождество и, кроме того, удовлетворяет краевым условиям.

Пусть в бесконечном стержне с нулевой начальной температурой, (рис. 1.2) в начальный момент времени 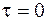в точке x=x¹ вспыхнул и мгновенно погас источник тепла, выделивший количество тепла Q.

Граничные условия могут быть записаны в виде

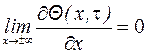(1.19)

Это указывает на отсутствие теплообмена между стержнем и окружающей средой на бесконечности.

Решение уравнения теплопроводности для мгновенного точечного источника тепла предложено У.Кельвином и имеет вид [1]

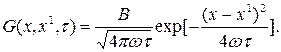(1.20)

Непосредственной проверкой можно убедиться, что функция (1.20) удовлетворяет уравнению теплопроводности (1.15) и граничным условиям (1.19). Из (1.20) следует, что функция 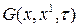имеет максимум в точке x=x¹ и что количество тепла Q в любой момент времени остаётся неизменным и равным C_v·В, а также, что величина B представляет собой площадь, ограниченную функцией 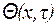и осью x.

Функцию 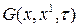называют фундаментальным решением уравнения теплопроводности. С помощью этого уравнения можно сконструировать решение

уравнения теплопроводности для других краевых условий: для этого любой процесс распространения тепла в твёрдом теле теплопроводностью представляется как совокупность процессов выравнивания температуры от множества элементарных источников тепла, распределённых как в пространстве, так и во времени. Результат получается суммированием (интегрированием) элементарных решений.

Рассмотрим метод быстродвижущих источников тепла. Быстродвижущими называются такие источники, скорость перемещения которых больше скорости распространения тепла. К быстродвижущимся источникам относят такие, для которых критерий Пекле: 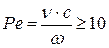, рис.1.3.

Здесь полуплоскость 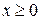, имеющая температуру 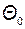, движется с постоянной скоростью V относительно оси y. На границе полуплоскости x=0 расположен равномерно распределённый теплоисточник, q=const, длина которого равна C. Суть метода быстродвижущихся источников тепла заключается в следующем: в среде, движущихся с большой скоростью V вдоль оси y относительно теплоисточника можно пренебречь переносом тепла за счёт теплопроводности вдоль этой оси.

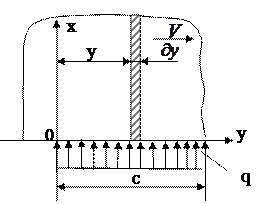
Из закона Фурье следует, что 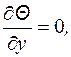а значит 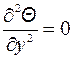. Таким образом, задача значительно упрощается, т.к. дифференциальное уравнение теплопроводности для двумерного поля (1.16) сводится к дифференциальному уравнению теплопроводности для одномерного поля (1.17) в полубесконечном стержне (заштрихованном) (рис.1.3), движущемся вдоль оси y относительно источника тепла q=const.