Законы электрических цепей
Раздел 2
Ветвь эл.цепи – называется участок цепи между двумя узлами
Узел эл.цепи – место соединения 3-х и более ветвей
Контур эл.цепи – это замкнутый путь для протекания тока
Независимый контур эл.цепи – это контур в который входит хотябы один новый элемент.
2.1 Закон Ома (в обобщённой форме)
Закон Ома применяется для расчёта токов и напряжений в отдельных ветвях цепи или для одноконтурной замкнутой цепи, не имеющей разветвлений.
При написании закона Ома следует прежде всего выбрать произвольно некоторое положительное направление тока.
Для ветви, состоящей только из сопротивлений и не содержащей ЭДС (см. рис.3.1. для ветви «ba»), при положительном направлении тока от (•) b к (•) a имеем:
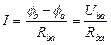 ,
,
где φb, φa – потенциалы точек (узлов a, b);
Uba – разность потенциалов между точками b и a;
Rba - эквивалентное сопротивление цепи, Rba = R1 + R2
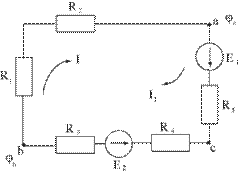
Рис.2.1.
Для ветви, состоящей из сопротивлений и ЭДС (ветвь acb), рис.2.1 ток равен:
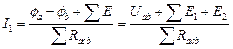 ,
,
где Uab – напряжение на концах ветви acb, отсчитываемое по выбранному положительному направлению тока;
ΣE – алгебраическая сумма ЭДС, находящаяся в этой ветви (Е1 + Е2)
2.2 Первый закон Кирхгофа
Первый закон Кирхгофа применяется к узлам электрической цепи. Он вытекает из принципа непрерывности электрического тока. Охватим узел цепи замкнутой поверхностью S (рис.2.2).
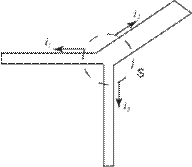
Рис.2.2.
В соответствии с принятыми допущениями вся электрическая ёмкость в цепи с сосредоточенными параметрами предполагается сосредоточенной в конденсаторах, включённых в цепь. Это соответствует пренебрежению токами электрического смещения, отходящими от соединительных проводов к другим участкам цепи. Таким образом, через замкнутую поверхность S проходят только токи проводимости в проводниках, пересекающих эту поверхность. Согласно принципу непрерывности тока в данном случае получим:
 ,
,
т. е. - сумма токов, расходящихся от узла электрической цепи, равна нулю.
 -плотность тока,
-плотность тока, 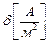
При любом числе ветвей имеем:  , т.е. алгебраическая сумма токов, расходящихся от узла электрической цепи, равна нулю.
, т.е. алгебраическая сумма токов, расходящихся от узла электрической цепи, равна нулю.
При составлении уравнений согласно первому закону Кирхгофа необходимо задаться условными положительными направлениями токов во всех ветвях, обозначив их на схеме стрелками. От узла, как правило, принимаем за положительное направление для токов, а знак «минус» приписываем токам, которые входят в узел. Для случая на рис.2.3 уравнение по первому закону Кирхгофа будет иметь вид:: - i1 + i2 + i3 = 0
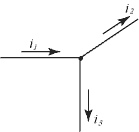
Рис.2.3.
Если в результате расчёта будет получено для некоторого тока в некоторый момент времени положительное число (ik > 0), то это значит, что ток имеет в данный момент времени действительное направление согласно стрелок. Если же будет получено ik < 0, то этот ток в действительности направлен против стрелки.
 2014-02-02
2014-02-02 680
680








