Применение законов Кирхгофа

1. Устанавливаются условно положительные направления токов в ветвях электрической цепи.

2. Выбираются независимые контуры (контур, содержащий хотя бы один новый элемент).

3. Определяется число уравнений по I закону Кирхгофа. Их число равно:

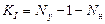
где Ny – число узлов электрической цепи;

Nн – число источников напряжений, если они расположены между узлами, не имеющими сопротивлений.

4. Составляются уравнения по I закону Кирхгофа;

5. Определяется число уравнений по II закону Кирхгофа:

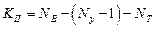
где N_B – число ветвей, Ny – число узлов;

N_T – число источников тока, если они расположены между узлами, не имеющими проводимостей.

6. Составляются уравнения по II закону Кирхгофа.

При составлении уравнений по II закону Кирхгофа следует выбирать независимые контуры, т.е. не содержащие источников тока.

Выбирается произвольное направление обхода контуров (произвольно).

При записи левой части равенства ЭДС, направления которых совпадают с выбранными направлениями обхода контура (независимо от направления тока, протекающего через них), принимаются положительными, а ЭДС, направленные против выбранного обхода, - отрицательными.

При записи правой части равенства со знаком «плюс» берутся падения напряжения в тех ветвях, в которых выбранное положительное направление тока совпадает с направлением обхода (независимо от направления ЭДС в этих ветвях), и со знаком «минус», падения напряжения в тех ветвях, в которых положительное направление тока противоположно направлению обхода контура.

2.5. Пример расчёта цепи постоянного тока с применением законов Кирхгофа

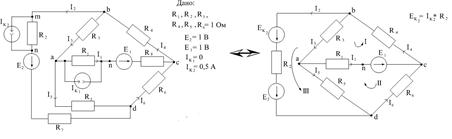
Рис. 2.5.

Решение:

КI = Ny – 1 – Nн = 4 – 1 – 0 = 3

Выбираем (•)a, (•)b, (•)c.

(•)a: I3 – I1–I5 = 0

(•)b: I4 – I2 – I3 = 0

(•)c: I6 + I1 – I4 = 0

KII = N_B – (Ny – 1) – N_T = 6 – (4 – 1) – 0 = 3

R3 I3 + R1 I1 + R4 I4 = E1 (I)

R1 I1 – R5 I5 – R6 I6 = E1 (II)

R2 I2 + R6 I6 + R4 I4 = E_k2+E2 (III)

К = КI +KII – общее число уравнений системы для определения токов I1÷I6. Решаем систему любым методом.

Вторым законом Кирхгофа можно пользоваться для определения напряжения между двумя произвольными точками схемы. В этом случае необходимо ввести в левую часть уравнений исходное напряжение вдоль пути, как бы дополняющего незамкнутый контур до замкнутого. Например, для определения напряжения Umn можно написать уравнение для контура mncb или nmbc:

2.6 Энергетические расчёты в цепях постоянного тока

При выполнении энергетических расчётов в цепях постоянного тока определяют следующие характеристики, связанные с распределением электрической энергии по элементам цепи:

- определение мощности, рассеиваемой в сопротивлениях цепи;

- определение суммарной рассеиваемой мощности;

- определение мощности, которую отдаёт в цепь источник напряжения или тока;

- проверку баланса мощностей.

Рассеиваемая мощность Pk характеризует способность сопротивления rk (или проводимость gk) необратимо преобразовывать электрическую энергию в любой другой вид энергии и рассчитывается по одной из формул:

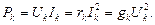
Суммарная рассеиваемая мощность для n сопротивлений и проводимостей определяется арифметической суммой мощностей, рассеиваемых в отдельных сопротивлениях rk или проводимостях gk цепи:

,

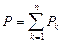где 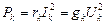- мощность, рассеиваемая в сопротивлении rk или проводимости gk, при этом направление напряжения или тока не влияет на рассеиваемую мощность.

В отличие от сопротивлений и проводимостей, которые способны только потреблять электрическую энергию, активные элементы (источники напряжения или тока) способны как потреблять, так и отдавать энергию во внешнюю цепь. В цепях с одним источником всегда происходит передача энергии источника во внешнюю цепь. При наличии в цепи нескольких источников некоторые из них могут работать в режиме потребления энергии. Такое положение может иметь место, например, при зарядке или разрядке аккумуляторов. В связи с этим мощность источников следует определять с учётом направлений напряжения и тока в них, пользуясь формулами:

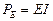или .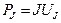

При положительных направлениях напряжения и тока источников, которые приведены на рис. 2.3, энергия источников передаётся во внешнюю цепь, и, следовательно, их мощность имеет положительное значение (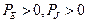). При отрицательных направлениях источники работают в режиме потребления энергии, и, следовательно, их мощность имеет отрицательное значение ().

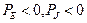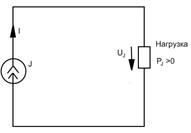
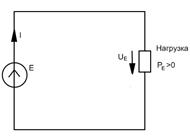
a) б)

Рис.2.6. К расчёту мощности источников напряжения (а) и тока (б)

Балансом электрических мощностей называют установление равенства мощностей, отдаваемых источниками во внешнюю цепь, и мощностей, потребляемых нагрузками.

Баланс мощностей можно установить с помощью формулы:

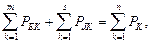
Где сравнивается сумма мощностей s источников тока Jk и m источников напряжения Ek (с учётом их знаков) с суммой мощностей Pk, потребляемых в n сопротивлениях rk или проводимостях gk цепи. При правильном решении задачи баланс мощностей соблюдается.

Пример 2.1. Требуется определить мощности источников энергии, мощности, рассеиваемые в сопротивлениях, и установить баланс мощностей для цепи, рассмотренной в примере 2.1. (рис.2.7.).

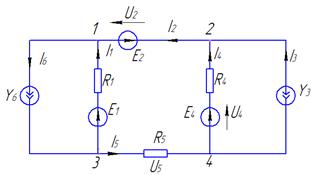
Рис.2.7.

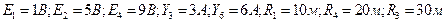
Решение. Решение задачи будем основывать на значениях токов и напряжений, полученных при решении примера 2.1.

Вначале определим мощность, которую отдают в цепь источники напряжения:

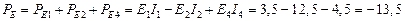Вт.

Из выполненного расчёта следует, что только источник E1 отдаёт энергию в цепь, а источники E2 и Е4 её потребляют.

Теперь определим суммарную мощность, которую отдают в цепь источники тока:

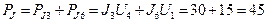Вт.

Из этого решения следует, что оба источника тока отдают энергию в цепь.

Полная мощность источников энергии:

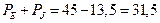Вт.

Наконец, определим мощность потерь в сопротивлениях цепи:

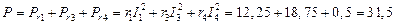Вт

Результаты расчёта показывают, что баланс мощностей выполняется.
Раздел 3