Подобие нагнетателей

Рис.2.5. Действительные характеристики.

Рис.2.4. Действительные характеристики.

Н_т (Q) - 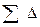Н (Q) = H (Q).

Методов, которые давали бы возможность получить функцию Н(Q), нет. Действительная кривая давления (напора) определяется только в результате аэродинамических испытаний. Во время этих испытаний также измеряется мощность, потребляемая турбомашинами, после чего не трудно найти действительный КПД.

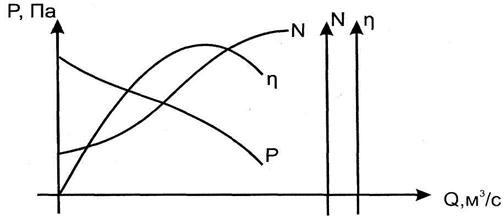
Полная характеристика турбомашин – это графики зависимостей Р, N, 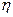=f (Q), напорная мощностная и обобщенная характеристика, построенная при постоянных значениях 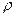, D, n.

Заводы-изготовители обычно прилагают к выпускаемой машине паспорт с характеристиками, представляющими зависимости

Р = f (Q) N = f^’ (Q) 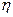=f^” (Q),

Кривые N =f (Q).

Передаваемую жидкости полезную мощность можно вычислить по формуле:

N_пол = Q P

из формулы видно, что N_пол.=0 при Q = 0 или Р= 0, т.е. в координатах N– Q кривая начинается от нуля (кривая I)

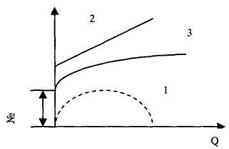
Но в связи с объемными потерями, а также из-за паразитной мощности, расходуемой на трение дисков лопаточного колеса о жидкость, кривая мощность лопаточных нагнетателей начинается не от 0, а несколько выше. Вид кривой зависит от конструкции нагнетателя (угла ₂). Если нагнетатель имеет лопатки, загнутые вперед (₁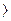90^о), то при производительности Q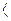Q_max(P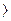P_дин.) кривая поднимается круто и непрерывно (кривая 2).

Для центробежных нагнетателей с лопатками, загнутыми назад, кривая имеет точку перегиба (кривая 3), причем величина мощности при оптимальном режиме оказывается близкой к максимальному ее значению. В точке пересечения кривой 3 с осью абсцисс мощность становится нулевой и дальше нагнетатель начинает не потреблять, а производить мощность, т.е. становится турбиной.

Так как у центробежных нагнетателей минимальная мощность соответствует нулевому расходу, то запускают их при закрытой регулировочной задвижке.

При построении кривой N = f^’ (Q) исходят из значений мощности на колесе, исключая механические потери в подшипниках и передаче. Мощность на колесе складывается из полезной, передаваемой жидкости (N_пол.), мощности, соответствующей гидравлическим потерям внутри нагнетателя

(N_пот.), мощности, соответствующей объемным потерям (перетекание жидкости через зазор – N_заз.), и паразитной мощности N_o

Кривые 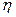=f (L).

Коэффициент полезного действия нагнетателя вычисляют по формуле

Q P

=------------

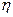N

откуда следует, что 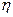= 0 при Q = 0 или при Р = 0

Таким образом, кривая 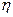=f (Q), имеет начальную точку в начале координат. Коэффициентом полезного действия характеризуется экономичность нагнетателей. В настоящее время есть опытные центробежные нагнетатели с 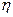= 0,9. Серийные нагнетатели простой и компактной конструкции имеют 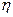= 0,6 – 0,7.

Производительность нагнетателя, соответствующая максимальному к.п.д. называется оптимальной и соответствующий режим работы нагнетателя оптимальным.

Подбор нагнетателей имеет целью – обеспечить их работу в оптимальном режиме. Применять нагнетатели в режимах работы 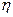= 0,9 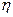_max не рекомендуется.

В тех случаях, когда динамическое давление нагнетателя теряется (например, при работе его на выхлоп), степень экономичности нагнетателя может характеризоваться не полным, а статическим к.п.д.

Q P_ст

=------------

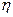N

Для построения кривой 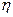=f (Q) на диаграмму наносят полученные в результате испытаний зависимости Р = f^’ (Q) и N = f^’ (Q) и для произвольно выбираемых Q берут из графиков N и P и подсчитывают .

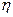По этим точкам и стоят кривую. Подсчитанные значения 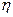не учитывают механических потерь в подшипниках и передаче, т.к. эти потери не учтены в N. Таким образом, к.п.д. относится к мощности на колесе.

Л Е К Ц И Я № 3.

Подобие нагнеталей.

План лекции:

3.1 Подобие нагнетателей.

3.2 Пересчеты характеристик при изменении частоты вращения и диаметре рабочего колеса, плотности жидкости.

3.2.1 Коэффициент быстроходности насосов или удельная частота вращения.

3.2.2 Универсальные характеристики.

В общем случае объекты считаются подобными, если процессы, протекающие в них, описываются одинаковыми системами уравнений и если для них характерно подобие условий однозначности, а также равенство критериев подобия.

Процессы в двух любых однотипных лопастных машинах, конечно, имеют одинаковую природу и, естественно, описываются одинаковыми системами уравнений. Однако, существенное различие между идеальными расчетными схемами и реальным рабочим процессом лопастных машин, потребовало разработки основ их экспериментального изучения на моделях и последующего обобщения результатов испытаний. Базой экспериментального метода изучения является классическая теория подобия физических явлений, которая применительно к лопастным машинам формулируется: разномасштабные геометрии подобные машины имеют сходные режимы, при которых выполняется кинематическое подобие в проточной части, а при определенных условиях – и динамическое подобие рабочих процессов.

Геометрическое подобие означает идентичность соотношений между всеми геометрическими размерами машин, составляющих серию (тип) подобных:

G₂

-------= i dem = 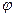_{2 1} = const ₂ = const

D₂

b₁ D₁

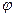₁=----= i dem, К_D = ------= i dem (6).

D₂ D₂

Машины геометрически подобны при следующих условиях6

- постоянным отношением входного диаметра колеса к внешнему диаметру;

- постоянным отношением ширины лопасти на входе к внешнему диаметру;

- одинаковых углах установки лопастей на входе в колесо; и выходе из колеса;

- одинаковой форме лопастей рабочих колес;

- одинаковой форме лопаток направляющего и спрямляющего аппаратов;

- одинаковой форме спиральных кожухов и соотношения их размеров.

При кинетическом подобии должно соблюдаться постоянство соотношений между скоростями потока в соответствующих сечениях рассматриваемых машин:

c u₂ w₂ v₂

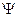= --------- i dem, -------- i dem ------= i dem

u₂ u₂ u₂

Динамическое подобие рабочих процессов означает идентичность соотношения между массовыми (центробежными) силами и силами вязкости. Критерием подобия при действии указанных сил является постоянство параметра Рейнольдса