Рис.2.1. Схема скоростей в рабочем колесе.
На рис.2. 1 плечо l1 равно длине отрезка 03, плечо l2 = 04.
Момент на валу:
М= m (c2 l2 - c1 l1) = r  Qв (c2 l2 - c1 l1),
Qв (c2 l2 - c1 l1),
где Qв – объемный расход (производительность), мз/с.
Из треугольников 013 и 024 видно, что l1=r1cos 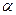 1; l2=r2cos
1; l2=r2cos 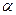 2.
2.
Тогда
М= 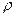 Qв (c2 r2 cos
Qв (c2 r2 cos 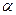 2 - c1 r1 cos
2 - c1 r1 cos 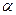 1).
1).
Выражая радиусы r1и r2 через угловую скорость  :
:
u1 u2
r1= -------; r2 = ------,


получим
М =
=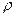 Q (u2 c2 cos
Q (u2 c2 cos 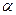 2 - u1c1 cos
2 - u1c1 cos 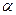 1 ).
1 ).
Произведение М равно теоретической мощности N = Qв
равно теоретической мощности N = Qв 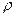 в.т.. Поэтому теоретическое давление (Па)
в.т.. Поэтому теоретическое давление (Па)
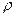 т.=
т.= 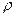 (u2 c2 cos
(u2 c2 cos 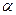 2 - u1c1 cos
2 - u1c1 cos 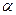 1 ). (2.1),
1 ). (2.1),
или, учитывая, что
Р
Н = --------, где
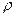 g
g
Н- напор, м; Р- давление, Па; 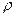 - плотность жидкости, кг/мз; g – ускорение свободного падения, м/с2
- плотность жидкости, кг/мз; g – ускорение свободного падения, м/с2
u2 c2 cos 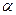 2 - u1c1 cos
2 - u1c1 cos 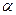 1
1
Н т= ----------------------------------------, или
g
u2 c2u- u1c1u
Нт= ------------------ (2.2),
g
c2u и c1u - скорости закручивания потоков
Из уравнения (2.1), называемого уравнением Эйлера, видно, что для получения максимального давления необходимо, чтобы второй его член в скобках был равен нулю. Это возможно, когда cos 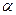 1 = 0, т.е. при
1 = 0, т.е. при 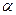 1=90о. Поэтому лопатки на входе изгибают против вращения на угол
1=90о. Поэтому лопатки на входе изгибают против вращения на угол  1
1 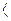 90о из условия
90о из условия 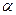 1=90о. В этом случае теоретическое давление вентилятора будет наибольшим, т.е.
1=90о. В этом случае теоретическое давление вентилятора будет наибольшим, т.е.
|
|
|
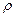 в.т.=
в.т.= 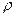 u2 c2 cos
u2 c2 cos 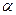 2 (2.3),
2 (2.3),
или
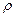 в.т.=
в.т.= 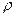
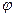 л u22,
л u22,
где 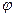 л – коэффициент закручивания лопаток, зависящий от их формы;
л – коэффициент закручивания лопаток, зависящий от их формы;
c2 cos 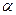 2 c2u
2 c2u
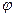 л = ---------------------= -----------
л = ---------------------= -----------
u2 u2
Из уравнения (2.1), называемого уравнением Эйлера, видно, что для получения максимального давления вентилятора необходимо, чтобы второй его член в скобках был равен нулю. Это возможно, когда cos 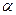 1 = 0, т.е. при
1 = 0, т.е. при 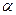 1=90о. Поэтому лопатки на входе изгибают против вращения на угол
1=90о. Поэтому лопатки на входе изгибают против вращения на угол  1
1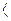 90о из условия
90о из условия 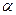 1=90о. В этом случае теоретическое давление вентилятора будет наибольшим, т.е.
1=90о. В этом случае теоретическое давление вентилятора будет наибольшим, т.е.
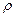 в.т.=
в.т.= 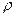 u2 c2 cos
u2 c2 cos 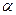 2
2
или
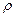 в.т.=
в.т.= 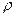
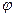 л u22,
л u22,
где 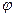 л – коэффициент закручивания лопаток, зависящий от их формы;
л – коэффициент закручивания лопаток, зависящий от их формы;
c2 cos 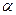 2 c2u
2 c2u
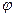 л = ---------------------= -----------
л = ---------------------= -----------
u2 u2
По форме лопатки бывают трех типов: радиальные, загнутые вперед и загнутые назад (рис.2.1). Для радиальных лопаток при  1 = 90о
1 = 90о 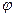 л = 1; для лопаток, загнутых вперед,
л = 1; для лопаток, загнутых вперед,  1
1 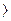 90о
90о 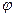 л
л 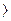 1; для лопаток, загнутых назад,
1; для лопаток, загнутых назад,  1
1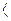 90о,
90о, 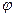 л
л 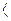 1.
1.
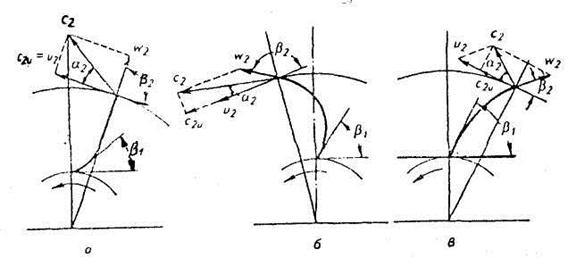
Рис. 2.2. Схема формы лопаток рабочих колес вентиляторов:
а - радиальные; б - загнутые вперед; в - загнутые назад.
Что касается входных кромок лопаток, то они всегда выполняются отогнутыми назад ( 1
1 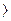 90о). При входной кромке, расположенной радиально, и в особенности при кромке, отогнутой вперед, резко возрастают гидравлические потери на вход жидкости в колесо.
90о). При входной кромке, расположенной радиально, и в особенности при кромке, отогнутой вперед, резко возрастают гидравлические потери на вход жидкости в колесо.
Зависимость между теоретической характеристикой Нт турбомашины и ее подача Qт при постоянной скорости вращения рабочего колеса и определенных геометрических размерах турбомашины называется индивидуальной характеристикой
Нт = f (Qт), которая может быть определена на основании известного уравнения
u2 cu2
Нт= ------------
g
из треугольников скоростей
Сu2 = u2 + cy2 ctg  2
2
Qт = 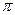 D2 b2cz2
D2 b2cz2
|
|
|
Q
cz2 = --------------
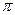 D2 b2
D2 b2
Q
Cu2 =u2 +-------------- ctg  2;
2;
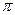 D2 b2
D2 b2
тогда
u2 ctg  2
2
Н т = --------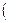 u2 + --------------- Q т) (2.4)
u2 + --------------- Q т) (2.4)
g 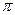 D2 b2
D2 b2
ctg  2
2
Н т = g u2 (u2 + --------------- Q т) (2.5)
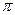 D2 b2
D2 b2
1
--- = 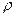 для вентиляторов.
для вентиляторов.
g
Как видно из уравнения теоретической индивидуальной характеристики, напор (давление) центробежного насоса Нт, при постоянной скорости вращения рабочего колеса и неизменных конструктивных размерах зависит от угла выхода лопатки 2, в зависимости от которого турбомашины делят на три типа:
2, в зависимости от которого турбомашины делят на три типа:
- с лопатками, загнутыми вперед, у которых  2
2 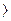 90о; ctg
90о; ctg  2
2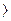 1;
1;
- с радиальными лопатками, у которых  2 = 90о; ctg
2 = 90о; ctg  2= 1;
2= 1;
- с лопатками, загнутыми назад, у которых  2
2 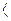 90о; ctg
90о; ctg  2
2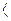 1.
1.
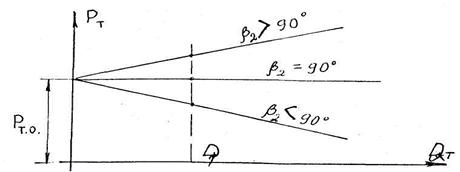
Уравнение теоретической индивидуальной характеристики для различных значений угла выхода лопатки  2 может быть выражено в координатных осях Нт - Qт линейной зависимостью при Qт = 0 уравнение для всех трех видов лопаток примет вид
2 может быть выражено в координатных осях Нт - Qт линейной зависимостью при Qт = 0 уравнение для всех трех видов лопаток примет вид
u22 u2 ctg  2
2
Н т = --------+ --------------- Q т
g 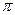 D2 b2 g
D2 b2 g
Теоретическая характеристика турбомашины, очевидно, представляет прямую линию. Свободный член в этом уравнении прямой, определяющий теоретическое давление при нулевом расходе, зависит только от окружной скорости колеса и не зависит от геометрии лопаток.
При Qт = 0 динамическое давление равно 0, а статическое давление равно Нт и создается центробежной силой. Машина работает на атмосферу, энергия потока равна 0.
 2014-02-02
2014-02-02 1742
1742








