В В Е Д Е Н И Е. 1.1. Геометрический аппарат проецирования и метод Г

С О Д Е Р Ж А Н И Е

В В Е Д Е Н И Е.. 4

1. КОМПЛЕКСНЫЙ ЧЕРТЕЖ НА ПРИМЕРЕ ИЗОБРАЖЕНИЯ ТОЧКИ.. 6

1.1. Геометрический аппарат проецирования и метод Г. Монжа получения обратимых изображений. 6

1.2. Комплексный чертеж точки. 8

1.3. Конкурирующие точки. 10

2. ОСНОВНЫЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ... 12

2.1. Способы задания геометрических фигур. 12

2.2. Прямая линия, плоскость и многогранник. 13

2.3. Кривая линия общего вида. 16

2.4. Кинематические поверхности. 16

3. ВЗАИМОПРИНАДЛЕЖНОСЬ ГЕОМЕТРИЧЕСКИХ ФИГУР. 19

3.1. Общие понятия взаимопринадлежности. 19

3.2. Точка на линии. 20

3.3. Прямая и точка на плоскости. 21

3.4. Точка и линия на поверхности. 22

4. ПЕРЕСЕЧЕНИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР. 25

4.1. Общие замечания. 25

4.2. Пересечение геометрических фигур, если одна из них – проецирующая. 26

4.3. Конические сечения. 29

4.4. Пересечение геометрических фигур с привлечением посредников. 30

4.4.1. Метод проецирующих секущих плоскостей. 32

4.4.2. Метод концентрических сфер. 35

4.4.3. Частный случай теоремы Г.Монжа. 37

5. ПРЕОБРАЗОВАНИЕ КОМПЛЕКСНОГО ЧЕРТЕЖА И СПОСОБ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА.. 37

5.1. Основные задачи преобразования. 37

5.2. Способ замены плоскостей проекций. 38

5.3. Способ вращения вокруг проецирующей прямой. 40

5.4. Способ прямоугольного треугольника. 41

6. ПАРАЛЛЕЛЬНОСТЬ И ПЕРПЕНДИКУЛЯРНОСТЬ ГЕОМЕТРИЧЕСКИХ ФИГУР. 43

6.1. Параллельность прямых и плоскостей. 43

6.2. Общие понятия перпендикулярности. 43

6.3. Перпендикулярность прямых и плоскостей. 44

6.4. Линия наибольшего наклона на плоскости. 46

7. МЕТРИЧЕСКИЕ ЗАДАЧИ.. 47

7.1. Классификация метрических задач (определение углов и расстояний) 47

7.2. Примеры решения метрических задач. 47

8. СТАНДАРТНАЯ ОРТОГОНАЛЬНАЯ АКСОНОМЕТРИЯ.. 50

8.1. Основные понятия. 50

8.2. Стандартная изометрия и диметрия. 50

8.3. Окружность в аксонометрии. 52

ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА. 54

Для тех, кто решил получить высшее образование, совершенно необходимо усвоить основной язык общения на производстве. Это язык инженерной графики. Теория изображения пространственных геометрических фигур на плоскости и практика выполнения технических чертежей излагаются в курсах начертательной геометрии и машиностроительного черчения.

Что такое начертательная геометрия?

«Это что-то техническое» – ответит любой человек

«Это самый трудный предмет в 1-ом семестре» – скажет первокурсник.

«Это наука, без знания которой невозможно техническое творчество» - уверенно ответит любой инженер*.

При изучении начертательной геометрии требуется систематическая работа. И если напряжение ума не вызывает у студента негативных эмоций, то курс начертательной геометрии окажется для него хоть и строгой, но красивой и понятной наукой.

На первых порах студенту необходимо вспомнить по крайне мере:

– Условия задания в пространстве простейших геометрических фигур: точки, прямой и плоскости.

– Условия взаимной принадлежности геометрических фигур таких как: точки и прямая на плоскости, точка и линия на кривой поверхности.

– Условия перпендикулярности: перпендикулярность прямой и плоскости, перпендикулярность двух плоскостей

– Теорему Фалеса.

– Теорему о трех перпендикулярах.

– Инвариантные (неизменные) свойства ортогонального проецирования (Рис.1):

1. Проекция точки есть точка.

2. Проекция прямой есть прямая(в общем случае).

3. Точка на прямой проецируется в точку на проекции этой прямой.

4. Проекции параллельных прямых – параллельны.

5. Относительно проекций параллельных отрезков равно отношению длин самих отрезков.

–––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––

*С.А. Фролов, М.В. Покровская «Начертательная геометрия. Что это такое?» - Минск, Высшая школа, стр. 5, 1986г.

6. Длина изображения отрезка, параллельного плоскости проекций, равна длине самого отрезка.

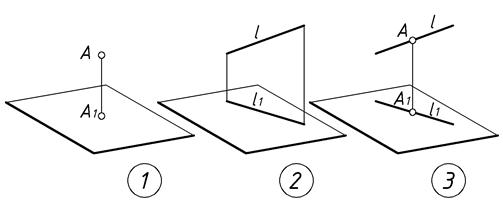7. Прямой угол проецируется без искажения, если одна сторона угла параллельна плоскости проекций, а вторая – не перпендикулярна к ней.

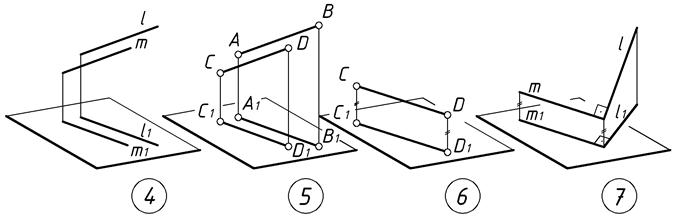Рис.1

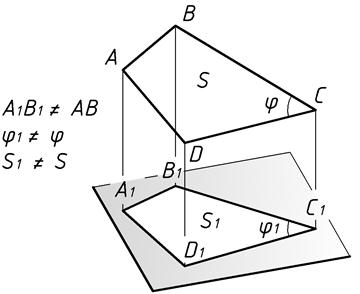Рис.2

На основе перечисленных инвариантных свойств, сформулированы основные законы начертательной геометрии. Эти законы устанавливают соответствие между изображаемой фигурой и её проекцией, когда геометрические свойства предмета в процессе проецирования отражаются с искажением (Рис.2). Искажается длина произвольно расположенного отрезка, искажаются углы и площади плоских фигур.

В чём заключается цель изучения начертательной геометрии:

1. Научится грамотно и осознанно работать с чертежами пока еще абстрактных геометрических фигур, а также - и решать такие задачи как:

– Изображение на комплексном чертеже точек, линий, плоских фигур и криволинейных поверхностей.

– Решение позиционных задач, связанных с принадлежностью и пересечением геометрических фигур, а также параллельностью и перпендикулярностью.

– Решение метрических задач на определение расстояний, углов и площадей плоских геометрических фигур.

2. Подготовить теоретическую базу для усвоения курса машиностроительного черчения и успешного выполнения технических чертежей, обладающих:

– обратимостью (однозначностью прочтения),

– наглядностью,

– простотой (предельной лаконичностью) и

– точностью исполнения.

3. Способствовать развитию у студента пространственного воображения.