Геометрический аппарат проецирования и метод Г. Монжа получения обратимых изображений

КОМПЛЕКСНЫЙ ЧЕРТЕЖ НА ПРИМЕРЕ ИЗОБРАЖЕНИЯ ТОЧКИ

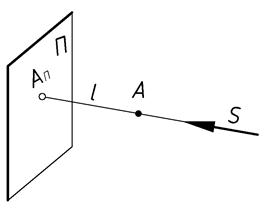Рис.3

В начертательной геометрии и в черчении для построения изображений в основном используется один из методов проецирования. Когда направление взгляда наблюдателя перпендикулярно к плоскости проекций, относительно которой сам наблюдатель условно находится на бесконечно удаленном расстоянии (Рис.3). Проецирующий луч 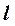от глаза наблюдателя 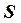проходит через точку 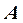какой-либо фигуры в пространстве и пересекает плоскость проекций 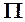, образуя ортогональную (прямоугольную) проекцию 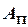. (Символически: ).

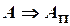Однако 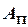– еще не чертеж. Чертеж должен читаться однозначно, то есть должен быть обратимым. В данном случае проекции 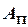может соответствовать не только точка 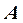, но и любая точка 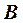, принадлежащая проецирующему лучу l. В итоге: 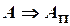, но .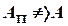

Способ получения обратимых изображений был предложен создателем начертательной геометрии как науки Гаспаром Монжем (1746-1818). Для этого оказалось достаточно: предмет спроецировать одновременно на две плоскости проекций. Например, - на две взаимно перпендикулярные плоскости: 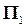– горизонтальную и 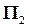– фронтальную плоскости проекций (Рис.4). В этом случае на лицо обратимость 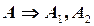и .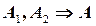

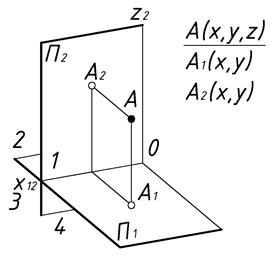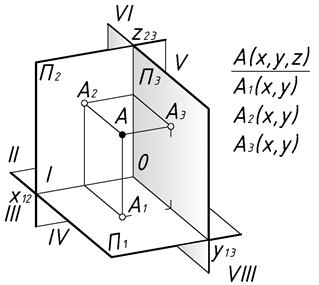Рис.4	Рис.5

Для усиления наглядности изображений и для решения многих геометрических задач часто приходится проецировать предмет на три плоскост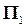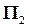и: , и 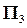. Последняя из них – профильная плоскость проекций (Рис.5).

Линии пересечения плоскостей проекций называются осями проекций. На этих осях происходит излом линий связи между отдельными проекциями точек. Звенья ломаных линий отражают расстояния точки в пространстве до соответствующих плоскостей проекций. Если оси проекций совместить с осями ортогональной системы координат 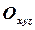, то эти расстояния примут свои численные значения. (Рис.4 и 5).

Плоскости проекций делят пространство на 4 квадранта плоскостям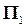и и 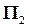и на 8 октантов – тремя плоскостями (Рис.4 и 5). От положения точки в той или иной части пространства зависят знаки её координат. Например, в I-м квадранте (Рис.4) все координаты положительны, во 2-м – координата 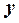уже отрицательна.

Что касается положения наблюдателя относительно плоскостей проекций: место наблюдателя или в 1-м квадранте или в 1-м октанте.

Пока мы получили только пространственные модели обратимых комплексных изображений на двух и на трех плоскостях проекций.