Положение о том, что точка на прямой проецируется в точку на проекции этой прямой (одно из инвариантных свойств проецирования) справедливо и для кривой
|
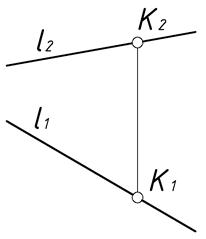
| Рис.29 |
линии. На комплексном чертеже это свойство должно проявляться, по крайней мере, на двух плоскостях проекций (Рис.29).
Задачи на принадлежность точки к прямой линии, как видно по чертежу, не вызывают особых затруднений. Кроме тех случаев, когда эта линия – линия уровня, заданная двумя проекциями с единственной линией связи. Как показано на Рис.30.
Если не строить третью проекцию, то для решения задачи приходится использовать теорему Фалеса. Смысл теоремы в том, что две прямые на плоскости делятся секущими параллельными прямыми на пропорциональные отрезки.
Пример (Рис.30). Построить недостающую (фронтальную) проекцию точки 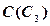 , принадлежащей отрезку
, принадлежащей отрезку 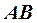 , параллельному плоскости
, параллельному плоскости 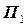 .
.
Дано:
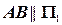
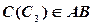 ______________
______________
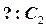 .
Решение:
1). .
Решение:
1). 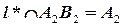 2).
2). 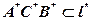 , где , где 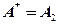
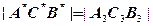 3).
3). 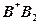 , , 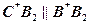 .
Проекция точки .
Проекция точки 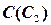 -искомая -искомая
|
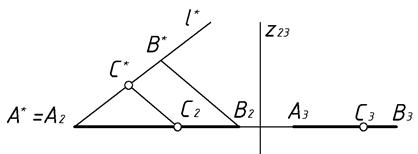
|
| Рис.30 |
Искомая проекция точки 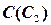 должна разделить фронтальную поверхность отрезка AB в таком же отношении, в каком отношении заданная проекция точки
должна разделить фронтальную поверхность отрезка AB в таком же отношении, в каком отношении заданная проекция точки 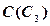 делит профильную проекцию этого отрезка:
делит профильную проекцию этого отрезка: 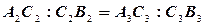 .
.
Воспользуйся теоремой Фалеса. Для этого на произвольной прямой 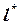 , пересекающей
, пересекающей 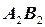 в точке
в точке 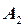 , отложим отрезок
, отложим отрезок 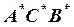 , равный профильной проекции отрезка
, равный профильной проекции отрезка 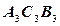 Проведя две параллельные прямые
Проведя две параллельные прямые 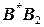 и
и 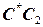 получим искомую проекцию точки
получим искомую проекцию точки 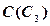 , поскольку обеспечены условия равенства отношений
, поскольку обеспечены условия равенства отношений 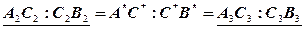
 2014-02-02
2014-02-02 685
685








