ПЕРЕСЕЧЕНИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР.
Пересечь геометрические фигуры – значит определить их общие точки и линии. И грамотно обвести чертеж с учетом видимости. Для этого совершенно необходимо хорошее усвоение пройденных тем таких, как принадлежность, особенности вырожденных проекций и видимость конкурирующих точек. Понадобится и теорема о пересечении соосных поверхностей вращения, разговор о которых пойдет несколько позже.
4.2. Пересечение геометрических фигур, если одна из них – проецирующая.
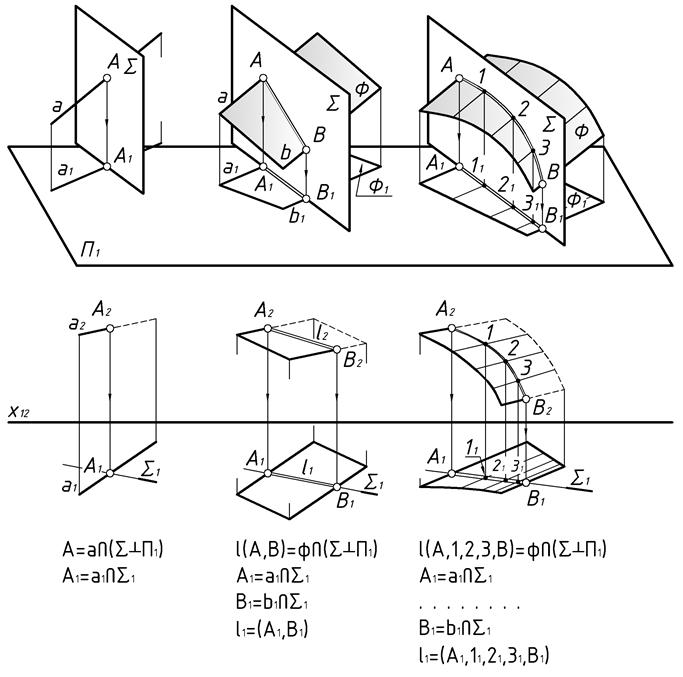
Наиболее легкий вариант пересечения геометрических фигур, если хотя бы одна их этих фигур задана проецирующей. На пространственных моделях проецирования и на комплексных чертежах (Рис.36) хорошо видно, что одну из проекций результата пересечения долго искать не надо. Результат накладывается или полностью совпадает с вырожденной проекцией одной из пересекающихся фигур. На комплексном чертеже остается только построить вторую проекцию результата пересечения. Используя принадлежность результата пересечения к пересекающейся фигуре общего положения.
 |
| Рис.36 |
При пересечении прямой общего положения с проецирующей плоскостью (Рис.36а) горизонтальная проекция точки их пересечения – в месте пересечения проекции прямой с вырожденной проекцией плоскости. На комплексном чертеже остается построить недостающую проекцию точки пересечения, используя известное положение о принадлежности точки к прямой общего положения.
При пересечении двух плоскостей, одна из которых – проецирующая (Рис.36б), горизонтальная проекция линии пересечения совпадает с вырожденной проекцией плоскости. Недостающая проекция линии пересечения строится по двум точкам, используя положение о принадлежности прямой к плоскости (в данном случае – к плоскости общего положения).
На Рис.36в принципиального отличия от предыдущего примера нет. Кроме того, что проецирующая плоскость пересекается с криволинейной поверхностью по кривой линии. Для построения второй проекции которой необходимо использовать достаточно плотный каркас из точек.
В рассмотренных примерах определение видимости можно определять без привлечения конкурирующих точек. Достаточно сопоставить положение вырожденной проекции относительно проекции второй фигуры и (условно) проекции наблюдателя.
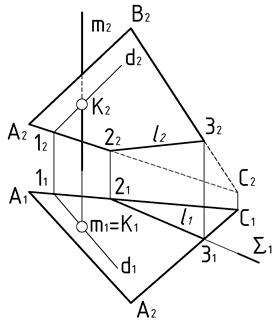
Пример 1 (Рис.37). Плоскость 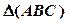 общего положения пересечь горизонтально проецирующими прямой
общего положения пересечь горизонтально проецирующими прямой 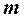 и плоскостью
и плоскостью 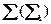 .
.
 |
| Рис.37 |
Дано: 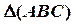 о.п., о.п., 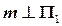 , , 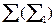 . ?: . ?: 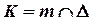 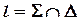 | Решение 1: 1). 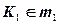 , 2). , 2). 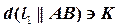 , 3). , 3). 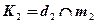 , 4). Видимость. Решение 2: 1). , 4). Видимость. Решение 2: 1). 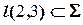 , 2). , 2). 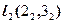 , 3). Видимость. , 3). Видимость. |
Прямая 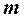 пересекает плоскость
пересекает плоскость 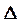 в точке
в точке 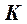 , горизонтальная проекция которой совпадает с вырожденной проекцией прямой
, горизонтальная проекция которой совпадает с вырожденной проекцией прямой 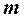 . Для построения фронтальной проекции искомой точки используем вспомогательную прямую, проходящую через саму точку
. Для построения фронтальной проекции искомой точки используем вспомогательную прямую, проходящую через саму точку 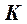 , задав ее точкой 1 и направлением, параллельным к одной из прямых, принадлежащих плоскости
, задав ее точкой 1 и направлением, параллельным к одной из прямых, принадлежащих плоскости 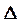 . Для определения видимости фронтальной проекции прямой m обращаем внимание на горизонтальную плоскость проекций. Понятно, что верхняя часть этой линии находится за прямой
. Для определения видимости фронтальной проекции прямой m обращаем внимание на горизонтальную плоскость проекций. Понятно, что верхняя часть этой линии находится за прямой 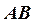 , принадлежащей плоскости
, принадлежащей плоскости 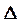 .
.
Следовательно, верхняя часть фронтальной проекции прямой 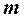 – не видима.
– не видима.
Горизонтально проецирующая плоскость 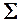 пересекает плоскость
пересекает плоскость 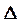 по линии
по линии 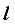 , горизонтальная проекция которой совпадает с вырожденной проекцией плоскости
, горизонтальная проекция которой совпадает с вырожденной проекцией плоскости 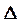 . Для построения фронтальной проекции линии пересечения используем две ее точки: 2 и 3 на линиях
. Для построения фронтальной проекции линии пересечения используем две ее точки: 2 и 3 на линиях 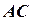 и
и 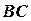 , принадлежащих плоскости
, принадлежащих плоскости 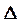 . Для определения видимости фронтальной проекции плоскости общего положения
. Для определения видимости фронтальной проекции плоскости общего положения 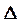 обращаем внимание на горизонтальную плоскость проекций. По которой судим, что часть треугольника с вершиной
обращаем внимание на горизонтальную плоскость проекций. По которой судим, что часть треугольника с вершиной 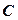 для наблюдателя не видна. Следовательно, фронтальная проекция этой части треугольника не видима.
для наблюдателя не видна. Следовательно, фронтальная проекция этой части треугольника не видима.
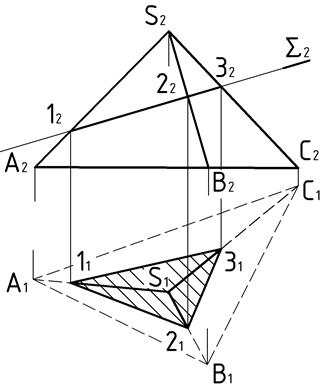
Пример 2 (Рис.38). Построить сечение пирамиды 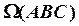 фронтально проецирующей плоскостью
фронтально проецирующей плоскостью 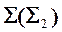 .
.
 |
| Рис.38 |
Дано: Пир. 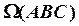 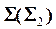 . _____________ ?: . _____________ ?: 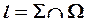 | Решение: 1). 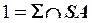 2). 2). 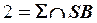 3). 3). 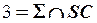 4). 4). 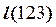 5). Видимость. 5). Видимость. |
Форма сечения – треугольник. Вершины треугольника – результат пересечения трёх рёбер пирамиды с проецирующей плоскостью.
Обратившись к фронтальной плоскости проекций можно определить, что нижняя часть пирамиды находится под проецирующей плоскостью. Следовательно горизонтальная проекция нижней части пирамиды – не видима.
Дано: Кон. 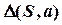 , Цил. , Цил. 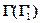 . _________ ?: . _________ ?: 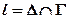 . . |
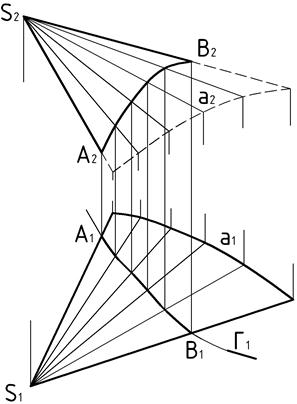
Пример 3 (Рис. 39). Построить линию пересечения конической поверхности 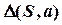 с горизонтально проецирующим цилиндром
с горизонтально проецирующим цилиндром 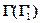 .
.
 |
| Рис.39 |
Горизонтальная проекция линии пересечения совпадает с вырожденной проекцией цилиндрической поверхности. Остаётся построить фронтальную проекцию этой линии. Решив по сути дела задачу на принадлежность кривой линии к поверхности конуса при наличии ее одной проекции. Для этого на поверхности конуса необходимо задать каркас из прямолинейных образующих, построить точки пересечения линии с элементами каркаса и по фронтальным проекциям этих точек провести недостающую проекцию линии пересечения.
Видимость фронтальной проекции конуса определяется путем обращения к горизонтальной плоскости проекций.
 2014-02-02
2014-02-02 2062
2062
