2014-02-02
4221
Мультиколлинеарность – это нарушение первой предпосылки линейной модели множественной регрессии о независимости факторных переменных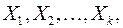 
включенных в модель. Мультиколлинеарность в матричном виде – это зависимость между столбцами матрицы факторных переменных 
Основная причина мультиколлинеарности заключается в неправильном подборе факторных переменных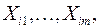 
включенных в модель. Последствия, к которым может привести наличие мультиколлинеарности в модели множественной регрессии:
1). основная гипотеза о незначимости коэффициента множественной регрессии в большинстве случаев подтверждается, однако сама модель регрессии при проверке с помощью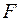 
- критерия оказывается значимой;
2). полученные оценки коэффициентов модели множественной регрессии неоправданно завышены или имеют неправильные знаки;
3). добавление или исключение е из исходных данных одного-двух наблюдений оказывает сильное влияние на оценки коэффициентов модели регрессии;
4). наличие мультиколлинеарности в модели множественной регрессии может сделать ее непригодной для дальнейшего применения (например, для построения прогнозов).
С целью мультиколлинеарности анализируют корреляционную матрицу факторных переменных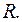 
Корреляционная матрица факторных переменных – это симметричная относительно главной диагонали матрица линейных парных коэффициентов корреляции факторных переменных:
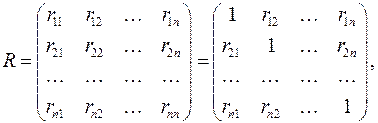
где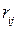 
- коэффициент парной линейной корреляции между 
и 
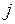факторными переменными 
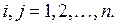Если в корреляционной матрице факторных переменных есть парный коэффициент корреляции между - ой и 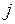- ой переменными 
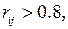то в модели множественной регрессии присутствует мультиколлинеарность, и в уравнении регрессии следует включать только один из показателей 
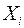или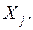 
Если собственное число корреляционной матрицы факторных переменных 
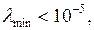то в модели множественной регрессии присутствует мультиколлинеарность. Если отношение собственных чисел корреляционной матрицы факторных переменных: 
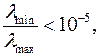то в модели множественной регрессии присутствует мультиколлинеарность. Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов между факторами. Если бы факторы не коррелировали друг с другом, то матрица парных коэффициентов корреляции между факторами была бы единичной матрицей, поскольку все ее недиаагональные элементы 
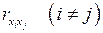были бы равны нулю. Если же наоборот, между факторами существует полная линейная зависимость и все коэффициенты корреляции равны 1, определитель такой матрицы 
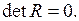Чем ближе к нулю определитель парных коэффициентов корреляции, тем сильнее мультиколлинеарность факторов и тем ненадежнее результаты множественной регрессии. И наоборот, чем ближе к единице определитель межфакторной корреляции, тем меньше мультиколлинеарность факторов.
