2014-02-02
2040
Статистические свойства МНК-оценок
Сумма квадратов остатков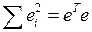 
является «кандидатом» на оценку дисперсии ошибок 
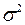(с некоторым коэффициентом):
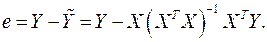Вычислим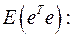 
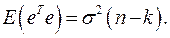(7)
Из уравнения (5.7)(7 ) следует, что
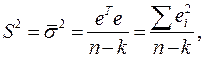(8)
т.е.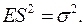
Поскольку 
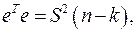следовательно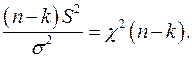 
Получаем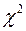 
-распределение с 
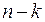степенями свободы.
Проверка гипотезы о значимости модели множественной регрессии состоит в проверке гипотезы о значимости множественного коэффициента корреляции или значимости коэффициентов модели регрессии. В большинстве случаев значимость модели множественной регрессии проверяется через значимость коэффициента множественной корреляции.
Основной гипотезой, выдвигаемой при проверке значимости коэффициентов регрессии, является гипотеза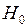 
о незначимости полученных коэффициентов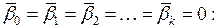 
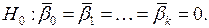
Обратной является гипотеза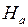 
о значимости коэффициентов регрессии: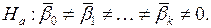 
Гипотезы проверяются с помощью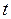 
-статистики или 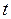-критерия Стьюдента, который рассчитывается через частный 
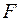-критерий Фишера. Между этими критериями существует взаимосвязь, используемая при проверке значимости коэффициентов модели множественной регрессии: 
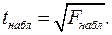Критическое значение 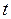-критерия: 
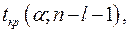где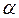 
- уровень значимости; 
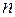- объем выборки; 
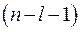- степень свободы, определяемая по таблице распределений 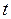-критерия Стьюдента.
Наблюдаемое значение частного 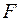-критерия для проверки гипотезы:
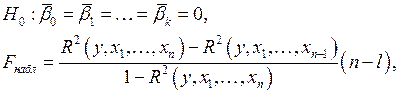
где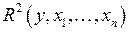 
- коэффициент множественной детерминации.
Если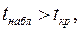 
то основная гипотеза о незначимости модели множественной регрессии отклоняется. Если 
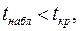то основная гипотеза о незначимости коэффициентов модели множественной регрессии принимается.
