Если при прогнозировании результативной переменной величина ошибки прогноза является удовлетворительной, то модель множественной регрессии можно использовать и при наличии мультиколлинеарности. Если же прогноз получается неудовлетворительным, то мультиколлинеарность необходимо устранить.
Сбор дополнительных данных – это самый простой способ устранения мультиколлинеарности. Однако на практике это не всегда возможно.
Метод преобразования переменных – это способ замены всех переменных, включенных в модель. Например, вместо значений результативной переменной и факторных переменных можно взять их логарифмы. Тогда модель множественной регрессии имеет вид:
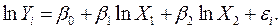 Однако этот метод не гарантирует устранения мультиколлинеарности.
Однако этот метод не гарантирует устранения мультиколлинеарности.
Гребневая регрессия (или ридж) − это один из смещенных методов оценки коэффициентов модели регрессии. Данный метод применяется в случае, когда ни одну из переменных, включенных в модель регрессии, нельзя удалить. Суть гребневой регрессии заключается в том, что ко всем диагональным элементам корреляционной матрицы 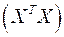 добавляется число
добавляется число 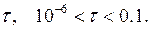 Тогда неизвестные коэффициенты модели множественной регрессии будут определяться по формулам:
Тогда неизвестные коэффициенты модели множественной регрессии будут определяться по формулам: 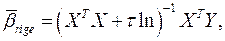 где
где 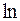 - единичная матрица. Гребневая регрессия позволяет стабилизировать оценки коэффициентов модели множественной регрессии к определенному числу и уменьшить их стандартные ошибки.
- единичная матрица. Гребневая регрессия позволяет стабилизировать оценки коэффициентов модели множественной регрессии к определенному числу и уменьшить их стандартные ошибки.
Метод главных компонент – это основной метод исключения переменных из модели регрессии. В этом случае модель множественной регрессии строится не на основе факторных переменных 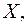 а на основе матрицы главных компонент
а на основе матрицы главных компонент 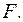
Метод пошагового включения – это метод определения из возможного набора факторных переменных именно тех, которые усилят качество модели регрессии. Суть метода пошагового включения состоит в том, что из числа факторных переменных в модель регрессии включаются переменные, имеющие наибольший модуль парного коэффициента корреляции с результативной переменной. При добавлении в модель регрессии новых факторных переменных их значимость проверяется с помощью 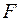 - критерия Фишера. Если
- критерия Фишера. Если 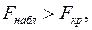 то включение факторной переменной в модель множественной регрессии является обоснованной. Проверка факторных переменных на значимость осуществляется до тех пор, пока не найдется хотя бы одна переменная, для которой не выполняется условие
то включение факторной переменной в модель множественной регрессии является обоснованной. Проверка факторных переменных на значимость осуществляется до тех пор, пока не найдется хотя бы одна переменная, для которой не выполняется условие 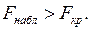
 2014-02-02
2014-02-02 2757
2757







