Рассмотрим n-мерное евклидово пространство 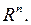
Пусть 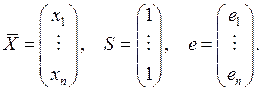
Введем обозначения: 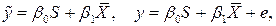 т.е.
т.е. 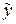 и
и 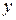 - векторы из
- векторы из 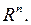 Тогда
Тогда
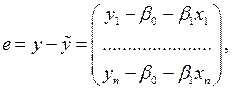
 – вектор, лежащий на двумерной плоскости
– вектор, лежащий на двумерной плоскости 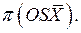 Предполагаем, что
Предполагаем, что 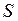 и
и 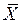 – неколлинеарны
– неколлинеарны 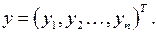
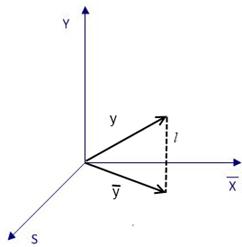 Поставим задачу: найти такие
Поставим задачу: найти такие 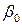 и
и 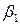 чтобы длина вектора
чтобы длина вектора 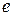 была минимальной, т.е. наилучшим образом аппроксимировала вектор
была минимальной, т.е. наилучшим образом аппроксимировала вектор 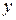 вектором
вектором 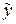 лежащим в плоскости
лежащим в плоскости 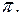 Очевидно, что длина
Очевидно, что длина 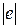 минимальна тогда и только тогда, когда вектор
минимальна тогда и только тогда, когда вектор 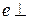 плоскости (кратчайшее расстояние от точки до плоскости есть перпендикуляр).
плоскости (кратчайшее расстояние от точки до плоскости есть перпендикуляр).
Но 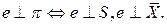
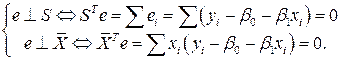 (9)
(9)
Нетрудно видеть, что (4) совпадает с (5), полученной по МНК. Введем обозначения:
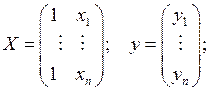
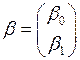 – вектор коэффициентов. Тогда:
– вектор коэффициентов. Тогда:
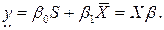
В самом деле:
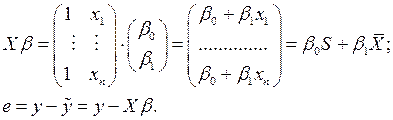
Условие ортогональности (9) можно записать следующим образом:
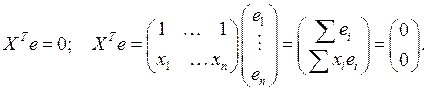
Запишем СЛАУ (9) более подробно: 
Умножим обе части на 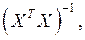 получим:
получим:
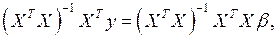
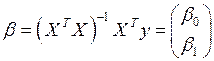 (10)
(10)
Замечание. Система (9) равносильна системе
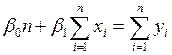

Формула (10) совпадает с формулами:
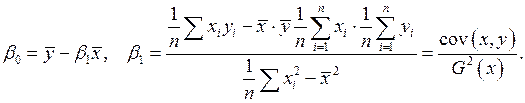
Оценка дисперсии ошибок σ2
В регрессионном уравнении есть еще один параметр – дисперсия ошибок σ2. Найдем оценку для этого параметра. Обозначим прогноз значения 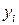 в точке
в точке 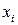 через:
через:
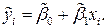 (11)
(11)
Остатки регрессии 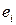 определяются из соотношения:
определяются из соотношения:
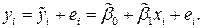 (12)
(12)
Замечание. Не следует путать остатки регрессии 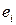 с ошибками регрессии в уравнении модели:
с ошибками регрессии в уравнении модели:
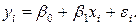 (13)
(13)
Разница состоит в том, что остатки 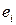 в отличие от ошибок
в отличие от ошибок 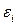 наблюдаемы. Имеем:
наблюдаемы. Имеем: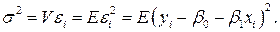 Естественно в качестве оценки
Естественно в качестве оценки 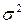 взять сумму:
взять сумму:
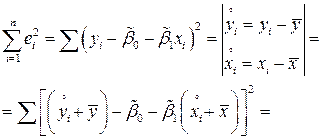
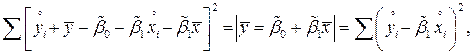
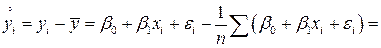
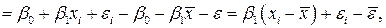
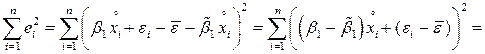
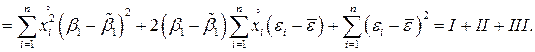
Вычислим матожидание 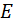 :
: 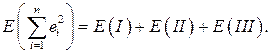
Без вывода:
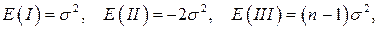
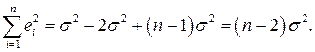
Отсюда 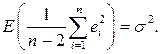
Итак, несмещенная оценка дисперсии случайной ошибки линейной модели парной регрессии рассчитывается по формуле:
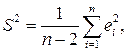
где n – объем выборочной совокупности; 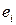 – остатки модели регрессии:
– остатки модели регрессии: 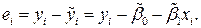
Предположим, что МНК – оценка любого коэффициента модели регрессии состоит из:
1) истинного значения коэффициента, т.е. константы;
2) случайной ошибки 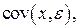 вызывающей вариацию коэффициента регрессии. Практически осуществить подобное разложение невозможно. Тем не менее можно доказать, что значение МНК-оценки зависит от величины случайной ошибки в модели регрессии.
вызывающей вариацию коэффициента регрессии. Практически осуществить подобное разложение невозможно. Тем не менее можно доказать, что значение МНК-оценки зависит от величины случайной ошибки в модели регрессии.
Формула для расчета МНК-оценки коэффициента модели регрессии 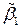 :
: 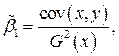
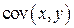 – ковариация между факторной переменной
– ковариация между факторной переменной 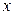 и результативной переменной
и результативной переменной 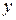 ;
; 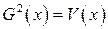 – дисперсия факторной переменной
– дисперсия факторной переменной 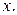
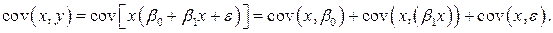
Свойства ковариации:
1). 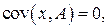 где
где 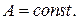
2). 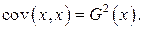
Исходя из свойства ковариации: 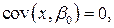 где
где 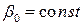 ;
;
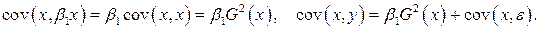
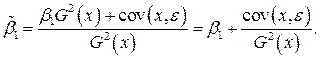
 2014-02-02
2014-02-02 712
712








