Сущность и значение средних величин, их виды
Наиболее распространенной формой статистического показателя является средняя величина. Показатель в форме средней величины выражает типичный уровень признака в совокупности. Широкое применение средних величин объясняется тем, что они позволяют и сравнивать значения признака у единиц, относящихся к разным совокупностям. Например, можно сравнивать среднюю продолжительность рабочего дня, средний тарифный разряд рабочих, средний уровень заработной платы по различным предприятиям.
Сущность средних величин заключается в том, что в них взаимопогашаются отклонения значений признака у отдельных единиц совокупности, обусловленные действием случайных факторов. Поэтому средние величины должны рассчитываться для достаточно многочисленных совокупностей (в соответствии с законом больших чисел). Надежность средних величин зависит также от колеблемости значений признака в совокупности. В общем случае, чем меньше вариация признака и чем больше совокупность, по которой определяется средняя величина, тем она надежнее.
|
|
|
Типичность средней величины непосредственным образом связана также с однородностью статистической совокупности. Средняя величина только тогда будет отражать типичный уровень признака, когда она рассчитана по качественно однородной совокупности. В противном случае метод средних используется в сочетании с методом группировок. Если совокупность неоднородна, то общие средние заменяются или дополняются групповыми средними, рассчитанными по качественно однородным группам.
Выбор вида средних определяется экономическим содержание ем исследуемого показателя и исходных данных. Наиболее часто в статистике применяются следующие виды средних величин: степенные средние (арифметическая, гармоническая, геометрическая, квадратическая, кубическая и т. д.), средняя хронологическая, а также структурные средние (мода и медиана).
Средняя арифметическая величина наиболее часто встречается в социально-экономических исследованиях. Средняя арифметическая применяется в форме простой средней и взвешенной средней.
Средняя арифметическая простая рассчитывается по несгруппированным данным на основании формулы (4.1):
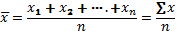
где x - индивидуальные значения признака (варианты);
n - число единиц совокупности.
Пример. Требуется найти среднюю выработку рабочего в бригаде, состоящей из 15 человек, если известно количество изделий, произведенных одним рабочим (шт.): 21; 20; 20; 19; 21; 19; 18; 22; 19; 20; 21; 20; 18; 19; 20.
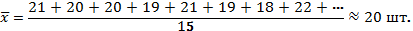
Средняя арифметическая простая рассчитывается по несгруппированным данным на основании формулы (4.2):
|
|
|
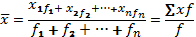
где f - частота повторения соответствующего значения признака (варианта);
∑f — общее число единиц совокупности (∑f = n).
Пример. На основании имеющихся данных о распределении рабочих бригады по количеству выработанных ими изделий требуется найти среднюю выработку рабочего в бригаде.
| Выработка деталей одним рабочим, шт., x | Число рабочих, чел., f | xf |
| ВСЕГО |
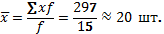
Примечание 1. Средняя величина признака в совокупности может рассчитываться как на основании индивидуальных значений признака, так и на основании групповых (частных) средних, рассчитанных по отдельным частям совокупности. При этом используется формула средней арифметической взвешенной, а в качестве вариантов значений признака рассматриваются групповые (частные) средние (xj).
Пример. Имеются данные о среднем стаже рабочих по цехам завода. Требуется определить средний стаж рабочих в целом по заводу.
| Номер цеха | Средний стаж работы, лет., X | Число рабочих, чел., f |
| ВСЕГО | - |
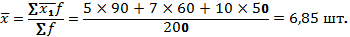
Примечание 2. В том случае, когда значения осредняемого признака заданы в виде интервалов, при расчете средней арифметической величины в качестве значений признака в группах принимают средние значения этих интервалов (х ’). Таким образом, интервальный ряд преобразуется в дискретный. При этом величина открытых интервалов, если таковые имеются (как правило, это первый и последний), условно приравнивается к величине интервалов, примыкающих к ним.
Пример. Имеются данные о распределении рабочих предприятия по уровню заработной платы.
| Группы рабочих по заработной плате, тыс.руб. | Число рабочих, чел., f | Средняя заработная плата, тыс.руб. x’ | x’f |
| До 250 250-350 350-450 450-550 550-650 650 и более | |||
| ВСЕГО | - |
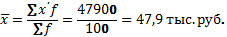
Средняя гармоническая величина является модификацией средней арифметической. Применяется в тех случаях, когда известны индивидуальные значения признака, т. е. варианты (x), и произведений вариант на частоту (xf = М), но неизвестны сами частоты (f).
Средняя гармоническая взвешенная рассчитывается по формуле (4.3):
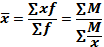
Пример. Требуется определить средний размер заработной платы работников объединения, состоящего из трех предприятий, если известен фонд заработной платы и средняя заработная плата работников по каждому предприятию.
| Предприятие | Фонд заработной платы, тыс. руб., xf | Средняя заработная плата, тыс. руб., x |
| 40 700 | ||
| 38 700 | ||
| 50 700 | ||
| ВСЕГО | - |
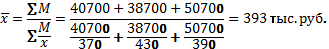
Средняя гармоническая простая в практике статистики используется крайне редко. В тех случаях, когда xf = Mm = const, средняя гармоническая взвешенная превращается в среднюю гармоническую простую (4.4):
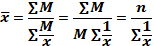
Пример. Две машины прошли один и тот же путь. При этом одна из них двигалась со скоростью 60 км/ч, вторая - со скоростью 80 км/ч. Требуется определить среднюю скорость машин в пути.
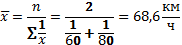
Другие виды степенных средних. Средняя хронологическая
Средняя геометрическая величина используется при расчете средних показателей динамики. Средняя геометрическая применяется в форме простой средней (для несгруппированных данных) и взвешенной средней (для сгруппированных данных).
Средняя геометрическая простая (4.5):
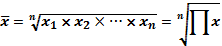
где n — число значений признака;
П — знак произведения.
Средняя геометрическая взвешенная (4.6):
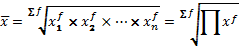
Средняя квадратическая величина используется при расчете показателей вариации. Применяется в форме простой и взвешенной.
Средняя квадратическая простая (4.7):
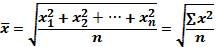
Средняя квадратическая взвешенная (4.8):
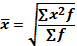
Средняя кубическая величина используется при расчете показателей асимметрии и эксцесса. Применяется в форме простой взвешенной.
Средняя кубическая простая (4.9):
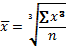
Средняя кубическая взвешенная (4.10):
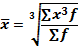
Средняя хронологическая величина используется для расчета среднего уровня ряда динамики (4.11):
|
|
|
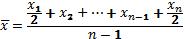
Структурные средние
Помимо рассмотренных выше средних величин в статистике используются структурные средние, к которым относятся мода и медиана.
Модой (Мо) называется значение изучаемого признака (вариант), которое чаще всего встречается в совокупности. В дискретном ряду мода определяется достаточно просто — по максимальному показателю частоты. В интервальном вариационном ряду мода приблизительно соответствует центру модального интервала, т. е. интервала, имеющего большую частоту (частость).
Конкретное значение моды рассчитывается по формуле (4.12):
где 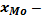 нижняя граница модального интервала;
нижняя граница модального интервала;
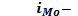 ширина модального интервала;
ширина модального интервала;
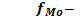 частота, соответствующая модальному интервалу;
частота, соответствующая модальному интервалу;
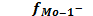 частота интервала, предшествующего модальному;
частота интервала, предшествующего модальному;
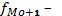 частота интервала, следующего за модальным.
частота интервала, следующего за модальным.
Медианой (Ме) называется значение признака, расположенное в середине ранжированного ряда. Под ранжированным понимают ряд, упорядоченный в порядке возрастания или убывания значений признака. Медиана делит ранжированный ряд на две части, одна из которых имеет значения признака не большие, чем медиана, а друга - не меньшие.
Для ранжированного ряда с нечетным числом членов медианой является варианта, расположенная в центре ряда. Положение медианы определяется порядковым номером единицы ряда в соответствии с формулой (4.13):
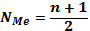
где n - число членов ранжированного ряда.
Для ранжированного ряда с четным числом членов медианой является среднее арифметическое из двух смежных значений, находящихся в центре ряда.
В интервальном вариационном ряду для нахождения медианы применяется следующая формула (4.14):
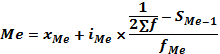
где 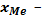 нижняя граница медианного интервала;
нижняя граница медианного интервала;
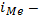 ширина медианного интервала;
ширина медианного интервала;
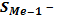 накопленная частота интервала, предшествующего медианному;
накопленная частота интервала, предшествующего медианному;
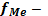 частота медианного интервала.
частота медианного интервала.
Пример. Рабочие бригады, состоящей из 9 чел., имеют следующие тарифные разряды: 4; 3; 4; 5; 3; 3; 6; 2;6. Требуется определить модальное и медианное значения тарифного разряда.
|
|
|
Поскольку в данной бригаде больше всего рабочих 3-го разряда, то этот разряд и будет модальным, т. е. Мо = 3.
Для определения медианы осуществим ранжирование исходного ряда в порядке возрастания значений признака:
2; 3; 3; 3; 4; 4; 5; 6; 6.
Центральным в этом ряду является пятое по счету значение признака. Соответственно Ме = 4.
Пример. Требуется определить модальный и медианный тарифный разряд рабочих завода по данным следующего ряда распределения.
| Разряд | Кол-во рабочих, чел. | Накопленная частота S |
| 13+25=38 38+30=68 68+19=87 87+10=97 97+3=100 | ||
| ВСЕГО |
Поскольку исходный ряд распределения является дискретным, то модальное значение определяется по максимальному показателю частоты. В данномпримере на заводе больше всего рабочих 3-го разряда (fmax = 30), т.е. этот разряд является модальным (Мо = 3).
Определим положение медианы. Исходный ряд распределения построен на основании ранжированного ряда, упорядоченного по возрастанию значений признака. Середина ряда находится между 50-м и 51-м порядковыми номерами значений признака. Выясним, к какой группе относятся рабочие с этими порядковыми номерами. Для этого рассчитаем накопленные частоты. Накопленные частоты указывают на то, что медианное значение тарифного разряда равно трем (Ме = 3), поскольку значения признака с порядковыми номерами от 39-го до 68-го, в том числе 50-е и 51-е, равны 3.
Пример. Требуется определить модальную и медианную заработную плату рабочих завода по данным следующего ряда распределения.
| Размер заработной платы, тыс.руб. | Кол-во рабочих, чел. | Накопленная частота S |
| 1 | 2 | 3 |
| 180-240 240-300 300-360 360-420 420-480 480-540 540-600 | 5 15 20 30 15 10 5 | 5 20 40 70 85 95 100 |
| ВСЕГО | 100 | 100 |
Поскольку исходный ряд распределения является интервальным, то модальное значение заработной платы рассчитывается по формуле. При этом модальным является интервал 360-420 с максимальной частотой, равной 30.
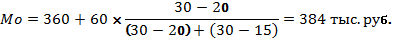
Медианное значение заработной платы также рассчитывается по формуле. При этом медианным является интервал 360-420, накопленная частота которого равна 70, тогда как накопленная частота предыдущего интервала составляла только 40 при общем числе единиц, равном 100.
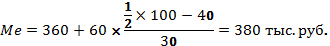
 2014-02-02
2014-02-02 26711
26711
