Эксцесс

Им также соответствуют выборочные характеристики: выборочный коэффициент вариации ,

выборочная асимметрия ,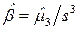

выборочный эксцесс .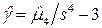

Все эти характеристики не совпадают с соответствующими характеристиками генеральной совокупности, поскольку являются случайными величинами. Распределение указанных случайных величин однозначно определяется распределением генеральной совокупности.

Точечными оценками параметров распределения называются функции от наблюдений, предназначенные для приближенного оценивания этих параметров. Если распределение параметризуется какими-то числовыми характеристиками (например, нормальное распределение однозначно задается своими математическим ожиданием и дисперсий), то соответствующие выборочные характеристики являются их точечными оценками.

Чтобы статистические оценки давали "хорошие" приближения оцениваемых параметров, они должны удовлетворять определенным требованиям. Эти требования заключаются в том, что оценка должна быть

состоятельной,

несмещенной

эффективной.

Оценка 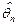называется состоятельной, если при неограниченном увеличении выборки она сходится по вероятности к оцениваемому параметру: 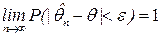для любого e > 0.

Оценка 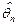называется несмещенной (оценкой без систематической ошибки), если ее математическое ожидание при любом n равно оцениваемому параметру: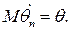

Оценка называется эффективной, если она имеет минимальную дисперсию в определенном классе оценок.

Пусть x имеет характеристики Мx= а, Dx=s², Мx^k=a_k, М(x–Мx)^k=m_k, F(x)=Р(x<х). Соответствующими выборочными характеристиками будут 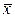, , 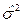s ², 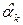, , 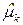F_n (x).

Докажем, что выборочные начальные моменты является несмещенной и состоятельной оценкой соответствующих теоретических начальных моментов. Для доказательства воспользуемся неравенством Чебышева 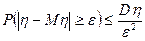, справедливом для любой случайной величины η и любого фиксированного ε>0.

Вычислим математическое ожидание и дисперсию выборочного начального момента:

,

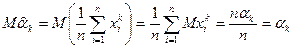так как 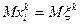. Отсюда следует, что выборочные начальные моменты являются несмещенной оценкой теоретических моментов.

Очевидно, что для любого k справедливо равенство

.

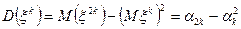Поскольку x_i независимы, то дисперсия суммы случайных величин x_i равна сумме их дисперсий

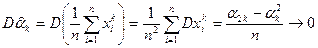при n®¥,

что является достаточным условием для сходимости по вероятности. Действительно, в силу неравенства Чебышева для любого фиксированного e>0 верно неравенство:

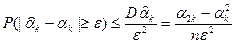®0 при n®¥,

то есть 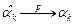и является состоятельной оценкой начального момента. Поскольку математическое ожидание случайной величины есть первый начальный момент Мξ=α₁, то из доказанного следует, 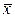является несмещенной и состоятельной оценкой математического ожидания.