В паутинообразной модели цена устанавливалась так, чтобы поглотить все предложение. Запасы товаров или отсутствовали или оставались неизменными. Модель можно расширить, учитывая наличие запасов. Можно выстроить следующую последовательность событий. Поставки товара вливаются в общую массу запасов, и фактический спрос удовлетворяется за счет запасов. В анализе появляется еще один субъект экономических отношений – продавцы товара. Таким образом, производители поставляют товар продавцам, имеющим запасы и реализующих товар, и покупатели. Действие модели начинается с продажи товара покупателям и установления цены в соответствии с размером запасов.
Для дискретного случая, если величина запасов в конце интервала 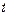 составляет
составляет 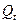 , то изменение запасов в течение этого интервала равно
, то изменение запасов в течение этого интервала равно 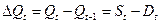 . В зависимости от особенностей установления цены, зависящей от величины запасов, можно построить несколько моделей.
. В зависимости от особенностей установления цены, зависящей от величины запасов, можно построить несколько моделей.
Модель 1. В период 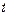 продавцы устанавливают цену
продавцы устанавливают цену 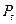 . Она больше цены
. Она больше цены 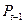 , если в предшествующий период запасы уменьшились. Цена повышается пропорционально сокращению запасов:
, если в предшествующий период запасы уменьшились. Цена повышается пропорционально сокращению запасов:  .
.
Модель 2. В период 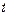 цена
цена 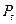 повышается, если в предшествующий период уровень запасов был ниже равновесного объема
повышается, если в предшествующий период уровень запасов был ниже равновесного объема 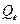 . Повышение цены пропорционально нехватке товаров до объема
. Повышение цены пропорционально нехватке товаров до объема 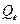 . Цена равна
. Цена равна 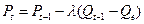 .
.
Модель 3 рассматривается в непрерывном анализе. В каждый момент времени продавцы устанавливают цену так, что скорость возрастания цены пропорциональна скорости уменьшения запасов:
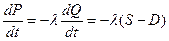 ,
,
где 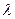 - положительная величина. Используем линейные функции спроса и предложения:
- положительная величина. Используем линейные функции спроса и предложения:  . Тогда имеем:
. Тогда имеем: 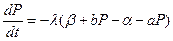 или
или
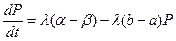 (1.7)
(1.7)
В точке равновесия 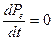 , поэтому
, поэтому
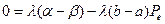 (1.8)
(1.8)
откуда находим равновесную цену 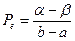 .
.
Вычитаем из уравнения (1.7) уравнение (1.8), получим: 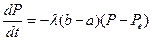 . Введем обозначение
. Введем обозначение  , тогда
, тогда 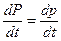 . Уравнение модели приобретает вид:
. Уравнение модели приобретает вид: 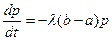 . Обозначим
. Обозначим 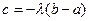 , тогда
, тогда  . В итоге имеем
. В итоге имеем 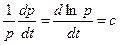 - дифференциальное уравнение относительно
- дифференциальное уравнение относительно 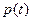 .
.
Используя правило логарифмического дифференцирования, нахождения производной логарифма сложной функции, получим: 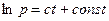 . Решение имеет вид:
. Решение имеет вид: 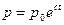 . При
. При 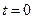 ,
,  . Следовательно,
. Следовательно, 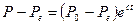
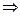
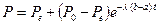 . Зная начальную цену, и подставив ее в функцию предложения, всегда можно найти объем продукции, который надо произвести.
. Зная начальную цену, и подставив ее в функцию предложения, всегда можно найти объем продукции, который надо произвести.
В случае нормальных товаров  ,
, 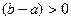 , и множитель
, и множитель  при
при 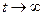 , стремится
, стремится 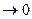 , а
, а 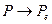 . Это справедливо для всех значений
. Это справедливо для всех значений 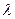 . Величина
. Величина 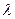 определяет скорость приспособления цены к изменению запасов. Чем больше
определяет скорость приспособления цены к изменению запасов. Чем больше 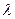 , тем быстрее
, тем быстрее 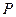 приближается к равновесной цене
приближается к равновесной цене 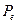 .
.
1.4. Устойчивость рыночного равновесия в концепции
 2014-02-02
2014-02-02 605
605








