Лекция8
Если каждой точке 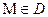 по некоторому правилу
по некоторому правилу 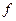 ставится в соответствие единственное действительное число
ставится в соответствие единственное действительное число 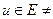 Ø, то
Ø, то 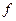 называют функцией, причем называют D – область определения функции; E– область изменения функции.
называют функцией, причем называют D – область определения функции; E– область изменения функции.
Точка 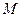 является аргументом функции. Правило
является аргументом функции. Правило 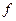 , однако, применимо не к самой точке, а к ее координатам.
, однако, применимо не к самой точке, а к ее координатам.
Таким образом, функция 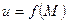 устанавливает связь между точками
устанавливает связь между точками 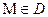 и точками некоторого множества одномерного пространства
и точками некоторого множества одномерного пространства 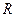 .
.
Область определения 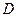 четной и нечетной функции симметрична относительно начала координат. Если это условие не выполнено, то функция не является четной и не является нечетной.
четной и нечетной функции симметрична относительно начала координат. Если это условие не выполнено, то функция не является четной и не является нечетной.
1) Функция 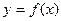 называется периодической, если существует такое положительное число Т, что при любом значении
называется периодической, если существует такое положительное число Т, что при любом значении 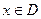 выполняется равенство
выполняется равенство
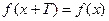 ,
,
число Т называют периодом функции.
2) Функция 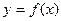 называется возрастающей на множестве
называется возрастающей на множестве 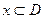 , если большему значению аргумента соответствует большее значение функции, то есть для любых
, если большему значению аргумента соответствует большее значение функции, то есть для любых 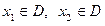 , таких, что
, таких, что 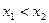 , выполняется неравенство
, выполняется неравенство 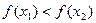 .
.
3) Функция 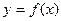 называется убывающей на множестве
называется убывающей на множестве 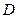 , если большему значению аргумента соответствует меньшее значение функции: если
, если большему значению аргумента соответствует меньшее значение функции: если
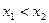 , то
, то 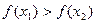 для любых
для любых 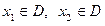 .
.
 2014-02-02
2014-02-02 359
359







