Их связь с бесконечно малыми

Рассмотрим функцию 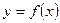, определенную на множество 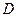, 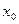- предельная точка множества .

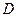Функция 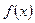называется бесконечно большой при 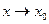, если для любого, даже сколь угодно большого положительного числа 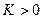, найдется такое положительное число 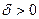(зависящее от 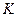, что для всех 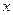, не равных 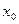и удовлетворяющих условию 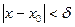, будет верно неравенство .

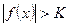Запись того, что функция 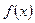бесконечно большая при 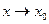, следующая:

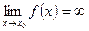
ил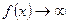и при .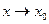

Краткая запись этого определения:

функция 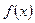бесконечно большая при 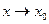, если для

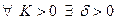, что 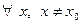; 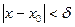выполняется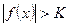

Для бесконечно больших функций имеют место следующие свойства.

Есл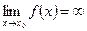и и 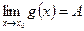, (, 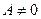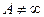), тогда

1)

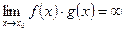
2)

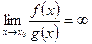
3) если 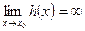, то

4) Связь между бесконечно малой 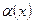и бесконечно большой 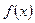функциями отметим в следующем свойстве:

если функция 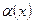есть бесконечно малая величина при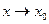 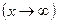, то функция 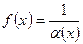является бесконечно большой при .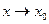

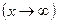И обратно, если функция 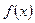бесконечно большая при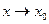 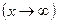, то функция 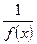есть величина бесконечно малая при .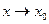

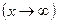То есть, если 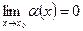, то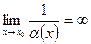

и наоборот, если 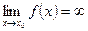, то .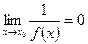

Например, 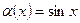является бесконечно малой при , тогда 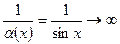, то есть является бесконечно большой при .