Декомпозицией схемы отношения R(A1, A2, …, An) называется замена ее совокупностью подмножеств {Ri} схемы R (подсхем) таких, что R1 ∪ R2 ∪ … ∪ Rk = R. При этом не обязательно, чтобы Ri были не пересекающимися.
Декомпозиция реализации отношения определяется как совокупность проекций отношения на подсхемы, полученные при декомпозиции схемы отношения. Так, если есть некоторая реализация отношения r(R), то, используя декомпозицию, получим:
ri = πRi(r), i = 1, 2, …, k.
Важно, чтобы декомпозиция была обратимой, т.е. выполнялась без потери информации: по проекциям отношения ri можно было бы восстановить исходную реализацию отношения r. Очевидно, что восстановление r из ri реализуется с помощью операции естественного соединения:
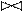
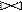
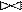 s = r1 r2 … rk
s = r1 r2 … rk
Где гарантия, что s ≡ r? Если такой гарантии нет, получив из ri s, мы не будем знать, достоверна информация или нет.
Рассмотрим пример. Пусть отношение со схемой S(S#, STATUS, CITY) имеет следующую реализацию:
| S | (S#, | STATUS, | CITY) |
| S1 | N1 | ||
| S2 | N2 |
Так как декомпозиция представляет собой проекцию отношения, рассмотрим следующие способы декомпозиции:
| a) | S1 | (S#, | STATUS) | S2 | (S#, | CITY) | |
| S1 | S1 | N1 | |||||
| S2 | S2 | N2 |
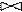 Делаем операцию естественного соединения – восстановление исходного отношения:
Делаем операцию естественного соединения – восстановление исходного отношения:
| s1 s2 = S | (S#, | STATUS, | CITY) |
| S1 | N1 | ||
| S2 | N2 |
Получили отношение, совпадающее с исходным.
| b) | S1 | (S#, | STATUS) | S2 | (STATUS, | CITY) | |
| S1 | N1 | ||||||
| S2 | N2 |
Восстанавливаем:
| s1 s2 = S | (S#, | STATUS, | CITY) |
| S1 | N1 | ||
| S1 | N2 | ||
| S2 | N1 | ||
| S2 | N1 |
В результате получили лишние строки, отсутствовавшие в исходном отношении.
Таким образом, возникает вопрос: как разбивать исходное отношение, чтобы не потерять информацию? Эта проблема получила название декомпозиции с соединением без потери информации. Вопрос о том, происходит ли потеря информации, тесно связан с функциональными зависимостями.
 2014-02-02
2014-02-02 367
367








