2014-02-02
510
Интерполяционный многочлен в форме Ньютона
Пусть f (x) – произвольный многочлен. Под разностью первого порядка будем понимать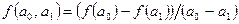 
. Индукцией определим разность порядка k 
.
.
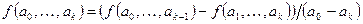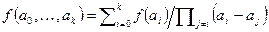Доказательство проведём индукцией по порядку разности. При k=1 имеем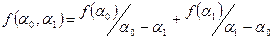 
. Основание индукции положено. Пусть утверждение верно для всех разностей порядка k-1. Покажем его справедливость для всех разностей порядка k. По определению 
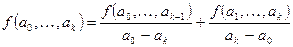. Подставим вместо разностей k-1 порядка их выражения, получим 
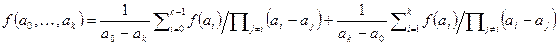После приведения подобных в правой части равенства получим требуемое утверждение.
Свойство 2
