Изоморфизм линейных пространств

Определение 7.13 Линейные пространства над числовым полем P называются изоморфными, если существует взаимно однозначное соответствие между векторами этих пространств, сохраняющее операции сложения векторов и умножения на скаляр.

Для доказательства изоморфизма линейных пространств V и W требуется построить взаимно однозначное отображение 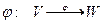, обладающее свойствами сохранения операции:

1. ,

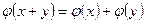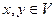
2. ,

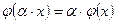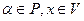
Следствие 7.10. При изоморфизме нулевой вектор переходит в нулевой вектор.

Доказательство. Действительно, .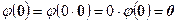

Лемма 7.3 Пусть V, W, U линейные пространства над полем P. Пусть W изоморфно V, а V изоморфно U, тогда W изоморфно U.

Доказательство. По условию существуют взаимно однозначные соответствия 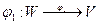и 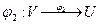, обладающие свойствами сохранения операции, то есть

1. ,

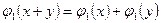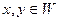
2. ,

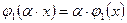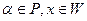
3. ,

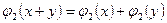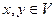
4. ,

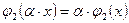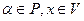
Отображение 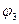, получаемое последовательным применением 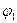и 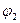, является взаимно однозначным соответствием между пространством W и пространством U. Далее, имеем

1. 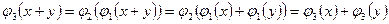, где .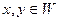

2. , .

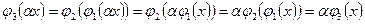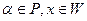Тем самым изоморфизм установлен.

Лемма 7.4 Пространство V над числовым полем P размерности n изоморфно арифметическому пространству .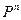

Доказательство. Пусть 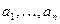- базис V. Каждому вектору x из V поставим в соответствие его координаты. Данное соответствие является взаимно однозначным (Теорема 7.4) и сохраняет операции. Тем самым изоморфизм установлен.

Лемма 7.5. При изоморфизме базис переходит в базис.

Доказательство. Пусть 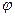- изоморфизм пространства V на W, 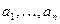- базис V. Разложим произвольный вектор x из V по базису 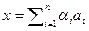. По определению изоморфизма 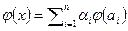, и значит, в силу взаимно однозначности отображения, через систему векторов 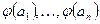линейно выражается любой вектор пространства W. Методом от противного покажем линейную независимость системы векторов 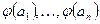. Пусть не так, тогда найдутся числа 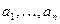, не все равные нулю, что 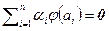. Последнее равенство, используя свойства изоморфизма, запишем в виде 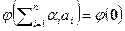. В силу взаимно однозначности изоморфизма выводим 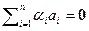, т.е. система векторов 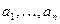- линейно зависима. К полученному противоречию с условиями нас привело допущение о линейной зависимости системы векторов 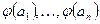. Таким образом, система векторов 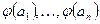является полной линейно независимой системой, т.е. базисом линейного пространства W.

Теорема 7.10. Линейные пространства V и W над полем P изоморфны тогда и только тогда, когда их размерности равны.

Доказательство. Если размерности пространств V и W совпадают и равны n, то оба пространства изоморфны 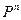(Лемма 7.4), а, значит и между собой (Лемма 7.3). Обратно, если пространства изоморфны, то при изоморфизме базис переходит в базис (Лемма 7.5), и, значит, размерности пространств равны.

Изоморфизм пространств позволяет переносить терминологию, принятую в одном пространстве на изоморфные пространства. Например, можно говорить о прямой в пространстве многочленов.