Уравнение движения точки и график движения

Лекция 10 Прямолинейное движение точки

Кинематика часть теоретической механики, в которой изучается движение механических систем, в частности движение твердого тела, независимо от сил, действующих на эти системы. Под механическим движением понимается изменение с течением времени относительного положения материальных тел. При изучении движения тела в кинематике его положение определяется по отношению к некоторой системе координат, связанной с другим телом, и называемой системой отсчета. Если положение данного тела по отношению к выбранной системе отсчета с течением времени остается неизменным, то это тело относительно этой системы отсчета находится в покое.

Кинематически определить движение тела – это значит указать его положение относительно выбранной системы отсчета в каждый момент времени.

Теоретическая механика рассматривает пространство, в котором происходят наблюдаемые движения материальных тел, как трехмерное эвклидово пространство и пользуется эвклидовой геометрией. Время в классической механике является универсальным, т.е. оно предполагается одинаковым во всех системах отсчета и не зависящим от относительного движения этих систем. С математической точки зрения время рассматривается в кинематике как непрерывно изменяющаяся величина, играющего роль независимого переменного (аргумента) и обозначается буквой t.

Изучение движения тела начинается с изучения движения отдельной точки, т.е. с кинематики точки. Линия, описываемая движущейся точкой в пространстве, называется траекторией точки. Если траектория точки – прямая линия, то движение точки называется прямолинейным, в противном случае движение называется криволинейным. Мы начнем изучать движение точки с наиболее простого случая - прямолинейного движения.

Пусть точка М описывает прямолинейную траекторию (рис.10.1). Примем эту прямую за ось х и будем определять положение точки на траектории ее абсциссой ОМ=х. Причем точка О есть произвольно выбранная на траектории неподвижная точка (начало координат).

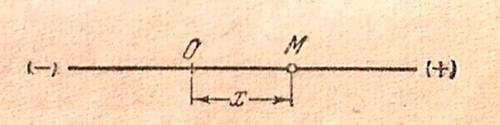Рис.10.1.

Так как при движении точки М каждому моменту времени (каждому числовому значению переменного t) соответствует единственное определенное положение этой точки на оси х и так как при перемещении точки М из одного положения в другое она последовательно проходит через все промежуточные положения, то абсцисса точки М является некоторой однозначной и непрерывной функцией времени, что в общем виде можно записать так: 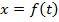(1)

Это уравнение называется уравнением движения или законом движения точки М по оси х. В зависимости от вида функции f мы будем иметь различные виды движения точки по прямолинейной траектории. Если известен закон движения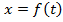, то для каждого произвольно выбранного момента времени можно найти соответствующее значение х и, следовательно, можем рассчитать положение точки М на ее траектории в любой момент времени. Таким образом, уравнение движения полностью определяет движение точки по заданной прямолинейной траектории.

Для наглядного представления о характере движения точки применяют графический способ. Уравнение движения на чертеже изображается, как функциональная зависимость между двумя переменными, между х и t. График функции 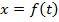, называется графиком движения или кривой расстояний.

По оси абсцисс откладываются значения времени как независимого аргумента t. Эта ось называется осью времени. По оси ординат откладывают значения пройденного расстояния х. Эта ось называется осью расстояний.

Масштаб изображения единиц времени и единиц расстояния выбирается произвольно. Давая различные числовые значения t, из уравнения движения находятся значения х. Получив ряд значений t и х, можно построить по этим координатам график движения точки. На рис.10.2 показан график прямолинейного движения точки, уравнение которого имеет вид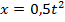

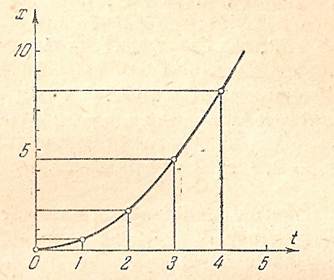Рис.10.2