Уравнения движения точки

Лекция 11 Криволинейное движение точки

Пусть точка М движется по заданной криволинейной траектории (рис.11.1).

Для того чтобы однозначно определить движение точки в данном случае, недостаточно знать ее траекторию, необходимо определить ее положение в любой момент времени. Выберем произвольно на данной траектории неподвижную точку О и будем определять положение движущейся точки М на траектории ее расстоянием от точки О, отсчитываемым по этой траектории, т.е. длиной дуги ОМ = s. Однако величиной дуги s положение точки М не определяется однозначно, так как мы можем выбрать разные направления движения и, следовательно, каждому значению s будут соответствовать два положения точки М на траектории. Для устранения этой двойственности установим на данной траектории направление отсчета дуг s и будем считать величину s алгебраической: если направление перемещения точки по траектории из положение О в положение М совпадает с выбранным положительным направлением отсчета дуг, то длину дуги 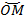будем считать положительной, в противном случае эту длину будем считать отрицательной. Алгебраическую величину s будем называть дуговой координатой точки М.

Так как в каждый момент времени точка М занимает вполне определенное положение на траектории, то каждому данному значению t соответствует единственное значение s. Другими словами, при движении точки ее дуговая координата s является функцией (однозначной и непрерывной) от времени t, т.е. 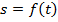(1)

Это равенство называется законом движения или уравнением движения точки по данной траектории. Если известны траектория точки и закон ее движения по этой траектории 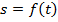, то движение точки вполне определено.

Другой кинематический способ определения криволинейного движения заключается в том, что положение движущейся точки в пространстве определяют ее тремя декартовыми координатами относительно выбранной неподвижной прямоугольной системы осей. При движении точки эти координаты являются однозначными и непрерывными функциями времени:

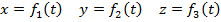(2)

Эти уравнения называются уравнениями движения точки в декартовых координатах. Ели функци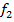и , и известны, то положение точки в пространстве для каждого момента времени полностью определено. Исключая время из этих уравнений, получим два соотношения между координатами, которые определяют линию, описываемую в пространстве движущейся точкой, т.е. ее траекторию.

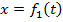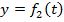Если движущаяся точка остается все время движения в одной и той же плоскости, то, приняв эту плоскость за координатную Оху, будем иметь только два уравнения движения: и (3)

Итак, криволинейное движение точки может быть определено двумя способами:

1. Известны траектория и закон движения ее по этой траектории, т.е. уравнение (1);

2. Известны уравнения движения точки в декартовых координатах, т.е. уравнения (2) или (3).

Для определения положения движущейся точки на плоскости можно пользоваться полярными координатами. Уравнения, выражающие полярные координаты в функциях времени, имеют вид:

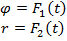
где φ – полярный угол, r – радиус вектор. Они называются уравнениями движения в полярных координатах. Исключив из этих уравнений время t, получим уравнение траектории точки в полярных координатах.