Пример 2. Необходимо извлечь выборку объёмом n=25 из распределения Стьюдента случайной величины xсматематическим ожиданием mx=10инеизвестнойдисперсией

Необходимо извлечь выборку объёмом n= 25 из распределения Стьюдента случайной величины x сматематическим ожиданием m_x=10 инеизвестнойдисперсией , определить интервал, в который с вероятностью 95% будет заключено выборочное среднее значение .

Из выражения (**) следует, что вероятность события

P (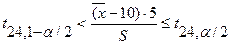 )=1-a

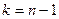=24

Из таблиц распределения Стьюдента для a= 0,05 находим .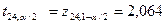

Для интервала 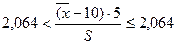границы будут следующими:

10-0,413∙S<£10+0,413∙S.

Точное значение ширины интервала для можно получить после извлечения выборки и определения S².

3.Распределение выборочной дисперсии.

Рассмотрим дисперсиювыборки объёма n независимых наблюдений случайной величины x.

S²=.

Пусть случайная величина x имеет нормальное распределение со средним значением и дисперсией .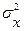

Укажем распределение выборочной дисперсии S². Дляэтого введём обозначение:

,

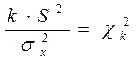где 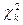- случайная величина, распределённая по закону 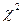- распределения с 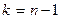степенями свободы.

Отсюда вытекает следующее вероятностное утверждение относительно S² до извлечения выборки.

P (> 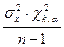)=a (***).

- это квантиль распределения уровня a.
Пример 3.

Для данных, приведённых в примере 1, определим интервал, который с вероятностью 95% будет покрывать выборочную дисперсию.

Из формулы (***) следует, что

.

Из таблицы 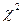- распределения находим значения квантилей

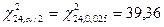
12,4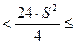39,36

- искомый интервал.