Раннее был рассмотрен вопрос об использовании выборочных оценок как численных параметров случайной величины, изученных на основе выборочных данных.
Однако такой способ позволяет получать лишь точечные оценки параметров. Более точный и надёжный способ оценивания параметров случайных величин заключается в определении интервала, а не единичного точечного значения. В этом случае необходимо определить интервал, в котором с заданной достоверностью будет заключено значение оцениваемого параметра.
Рассмотрим случай, когда среднее значение выборки n- наблюдений  используется в качестве оценки истинного среднего значения случайной величины x - m x.
используется в качестве оценки истинного среднего значения случайной величины x - m x.
Практически полезно находить для истинного среднего значения случайной величины x - mx такой интервал, в котором с некоторой степенью достоверности будет заключено это истинное среднее значение. Этот интервал можно найти, если известно выборочное распределение, используемое в качестве оценки выборочной величины.
Функцию выборки, которая используется для оценки того или иного параметра, называют статистикой.
Для нормально распределённой случайной величины с неизвестным средним значением и дисперсией, эту вероятность, характеризующую выборочное среднее значение  до извлечения выборки, можно определить следующим образом:
до извлечения выборки, можно определить следующим образом:
P (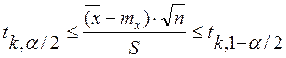 )=a,
)=a,
где 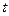 - соответствующий квантиль распределения Стьюдента.
- соответствующий квантиль распределения Стьюдента.
После извлечения выборки случайной величины x выборочное среднее значение  и дисперсия
и дисперсия 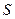 принимают определённые числовые значения, а не являются случайными величинами.
принимают определённые числовые значения, а не являются случайными величинами.
Следовательно, приведенное выше выражение для вероятности, уже не применимо, так как отношение

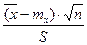
либо попадает, либо не попадает в указанные пределы.
Иначе говоря, после того как выборка извлечена, верное значение для вероятности имеет вид:
P (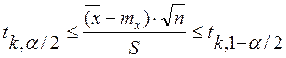 )=1,
)=1,
P (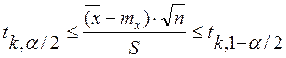 )=0,
)=0,
в зависимости от того, попадает или не попадает в указанные пределы.
Будет ли точечное значение вероятности равно 1 или 0, обычно не известно. Но если повторно извлекается большое число выборок и по каждой выборке вычисляется выборочное среднее значение  и стандартное квадратическое отклонение, то следует ожидать, что доля случаев, для которых отношение величин, входящих в приведённую формулу будет попадать в указанный интервал, примерно равна величине a. В таких случаях можно указать интервал, в который, как можно ожидать, отношение
и стандартное квадратическое отклонение, то следует ожидать, что доля случаев, для которых отношение величин, входящих в приведённую формулу будет попадать в указанный интервал, примерно равна величине a. В таких случаях можно указать интервал, в который, как можно ожидать, отношение
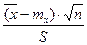
попадает с очень большой степенью вероятности.
Такой интервал называется доверительным интервалом.
Вероятность, с которой доверительный интервал включает оцениваемое значение параметра, называется доверительной вероятностью.
При оценке среднего значения доверительный интервал для истинного среднего значения mx можно получить по известным выборочным средним значениям  и
и 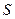 из соотношения
из соотношения 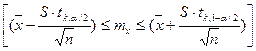 .
.
При выводе неравенства учитывается, что значение квантиля 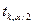 =
=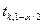 ,
,
где 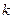 - число степеней свободы.
- число степеней свободы.
Доверительная вероятность, соответствующая приведённому выше интервалу, составляет 1- a. Следовательно, статистический вывод можно сформулировать следующим образом: истинное среднее значение mx попадает в данный интервал с доверительной вероятностью 1- a, илис доверительной вероятностью, равной 100∙(1- a).
Аналогичные статистические выводы можно сформулировать для оценок любых параметров, если известно соответствующее выборочное распределение, например, доверительный интервал для дисперсии 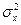 будет определяться как
будет определяться как
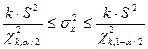 ,
,
n- число наблюдений
S2 - выборочная дисперсия
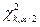 ,
,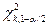 - соответствующие квантили
- соответствующие квантили 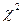 - распределения.
- распределения.
ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ.
 2014-02-02
2014-02-02 1550
1550

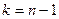 -
-